8.4 The Error Propagation of the SWS Pipeline

 

8.4.1 Introduction

This paper summarizes the error propagation of the SWS pipeline, based on pipeline version 6.0. During this study it turned out that it is possible to improve the error handling of this pipeline version. Thus a few modifications were done within the IA3 environment (SPR_S0166). Especially the DERIVE AAR s/w changed drastically in some cases of the error computation.

The computed errors in the Auto Analysis product do not reflect all known uncertainties to the `flux' value in the AAR. An attempt has been made to correctly propagate the detector noise through all steps of flux calibration, and to include other effects like the statistical error of dark current measurements. There are, however, effects like slow detector drifts which may significantly affect the measured flux but cannot be precisely quantified. The 'stdev' is hence more a number which might be suitable for comparison purposes, e.g. assessing which part of the spectrum are `more noisy', than for quantifying the absolute uncertainty in (continuum) flux.

Due to technical reasons it is not meaningful to compare errors of different detectors. It is more intended to give an impression about the relative errors for one detector.

8.4.2 DERIVE SPD

At constant illumination the output of the SWS detectors can be approximated as a voltage changing linearly with time;

An equation of the form:

The increase of this voltage (i.e. the slope  S) is dependent on the radiation falling onto the detector, the physical quantity of interest. In Derive-SPD a slope and offset  (O) are derived from the 24 Hz data for each reset interval. See sections 8.3.8, ``Flux calibration'' and 8.2.9, ``Extraction of the photo-currents and their uncertainties''.

To calculate the slope in the ISO detector data, we take the AC-corrected detector outputs for every reset interval versus time. Be aware that due to uncertainties in the AC-constants of every detector the slope might be slightly curved. This method to compute the error could give a sigma value even if the input before AC-correction is perfect. So the computed error is not suited to compare between detectors, moreover it represents the relative error of one detector.

As usual we write the -equation as

In the first instance the summation is over one second of data. Later, the equation can be re-summed over the complete reset interval. We want to find a minimum in . To this end we differentiate the equation to a and b and put both equations to 0: the normal equations.

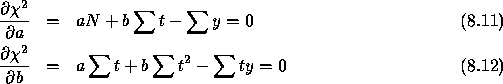
N : number of samples in 1 reset period

The solutions to this set of equations is

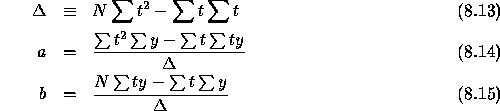
And:

The variance of the solution is and hence the standard deviation is:

N : number of samples

We can now calculate the formal errors in the offset and the slope.

The `standard deviation of the slope', was passed into the SPD product in field SWSPSTDV for OLP version 5.x.

Pipeline version 6.0 computes a slightly different `standard deviation of the slope', :

8.4.3 DERIVE AAR

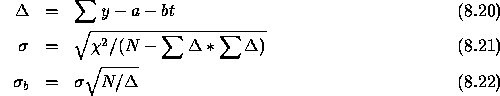
To understand the error handling of this part of the s/w it is unavoidable to mention some basics how the DERIVE AAR s/w is working. The DERIVE AAR part of the pipeline is noted step by step. Every section heading is starting with the related IA3 module call, a short explanations what this module should do is appended. In some cases the pipeline FORTRAN modules are mentioned to support pipeline module maintenance.

ANTIMEM : Remove memory effects

No error calculation done.

DARK : Dark Current subtraction

In the standard case a dark current measurement is precedes and follows a scan with the same gain and reset settings. The medians of this dark current measurements are used and applied to the scan data by linear interpolation.

Also, the actual dark is subtracted from the dark current itself. In some cases (old AOTs or to many bad data during dark current measurement) only one valid dark current measurement is taken for subtraction.

The square data of the `standard deviation of the slope', as given in the SPD are collected for the valid data of a dark current block:

Where N is the number of slopes in the dark current block.

After computing the median from the dark current block data a number suited for error propagation (delta_med) is returned:

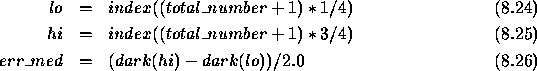
 total_number : total number of valid data points during dark block

index         		 : 		  ordered indices of dark current data block

dark  		 : 		 ordered array of slopes during dark current measurement

err_med 		 : 		 a width value which is used for error propagation (error of the
MEDIAN)

This calculation is done for every dark current block.

The error returned from the MEDIAN calculation and the error of the dark current block itself are combined to:

 

For the dark current block data itself the error is computed for each slope as:

For the scan data the flux and error for a reset interval is computed:

 

 

 err_out_data : new computed error

err_block   		 : 		 median of dark current data block before scan 
(equation 8.28)

err_block   		 : 		 median of dark current data block after scan (equation
8.28)

       		 : 		 error given with the input data (pipeline   )

ac_time       		 : 		 ITK of slope

time         		 : 		 ITK of dark current measurement before scan

time         		 : 		 ITK of dark current measurement after scan

RESPCAL : Responsivity Calibration

To aid understanding and to help maintain the pipeline code pipeline modules are named where calculations happen.

aas_read_conv_factors:

First the AOT band related calibration file 25 is read in. Calfile 25 contains the data of the RSRF (resfac) for several wavelength of an AOT band. Every calfile 25 entry is associated with a related error (reserr). How this error is computed is subject of the related CAP.
For a given key wavelength the related calfile 25 RSRF-factor (resfac_kw) is determined by searching in the array of data. Then a linear interpolation conserving the flux is applied to the calfile 25 data.

aas_fc_intpol:

The flux at key wavelength (resfac_kw) is the total integral of fluxes (obtained using the trapezoid rule) between flux at key wavelength minus FWHM and flux at key wavelength plus FWHM divided by FWHM. For AOT1 the FWHM is obtained from Cal-G file 19, for all other AOTs it is set to 0 and no division takes place

It is assumed that the error follows the same integration formulae as the fluxes (reserr_kw), except that the error is divided by the square root of a dilution factor being the ratio between the FWHM and the local stepsize in wavelength. Integrating over more wavelength's yields a smaller error while interpolating over a small part one wavelength interval a larger error.

aas_read_conv_factors:

Every array entry (resfac) is normalized to the computed factor at key wavelength (resfac_kw):

 

The errors of the normalized calfile 25 data are calculated in OLP V5 as:

The current IA3 system (and future OLP V6) computes the error differently:

aas_det_conv_factor:

For every wavelength the related table of resfac_n (equation 8.32) is searched and the actual value at the wavelength of interest is determined by linear interpolation, to produce resfac_ni. For AOT1 data Cal-G 19  is accessed and a special FWHM value is extracted. This value goes into the interpolation conserving the flux algorithm as above (err_ni). Errors are treated as before (aas_fc_intpol). For the simple linear interpolation (non AOT1 data), the error is also computed by linear interpolation (err_ni). Now the Cal-G 25  data are prepared to be applied.

aas_resp_cal:

Finally the new flux is computed:

 

 

 flux_out    : new computed flux

flux_in     		 : 		 flux input from equation 8.30

err_out     		 : 		 new error computed

err_in      		 : 		 error input from equation 8.31

The current IA3 implementation (and OLP V6) computes the error as:

And the new error:

FLUXCON : Flux Conversion

aas_det_lt_resp_factor:

The first photometric check is used to compute the reference value for flux conversion (flux_pm). For this purpose first a three value-box-car filter is applied on the photometric check data, the data are ordered (flux_p) and the median is taken.

N : number of data (reset intervals) of the photometric check

To calculate the error on the median a one point offset against the median is computed:

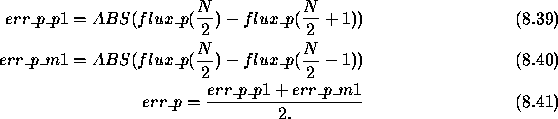
 err_p_p1   : plus one sample deviation against MEDIAN

err_p_m1   		 : 		 minus one sample deviation against MEDIAN

N            		 : 		 number of data of the photometric check

flux_p      		 : 		 ordered array of photometric check data

aas_read_cal_factor:

The relative flux data (rel_flux) and the error of the relative flux (err_13) are taken from calibration file 13, one per band. How to compute this error in the relative flux is described in the related CAP and is not part of this paper.

aas_flux_con:

The new flux and associated error are calculated for each reset interval by:

 flux_out    : new computed flux which is part of the AAR

flux_in     		 : 		 flux input from equation 8.35

err_out     		 : 		 new computed error which is part of the AAR

err_in      		 : 		 error input from equation 8.36

Also here the current IA3 system (and OLP V6) calculates the error differently:

VELCOR : Velocity Correction

This works on wavelengths alone, and no error calculation is done.

EXTRACT_AAR : AAR Extraction

No error calculation necessary, as this is just data extraction.