Source positions in 2MASS were reconstructed in the International Celestial Reference System (ICRS) via the Tycho-2 Reference Catalog.
Position reconstruction was accomplished in three steps. The first step was to reconstruct each scan individually using point source extractions within each frame to tie to the ACT Reference Catalog (Tycho-2 not yet available at that time) and simultaneously to tie the frames together. After all scans had been processed through the pipeline global scan overlap data became available. The second step was to divide each scan into 12 segments and treat each segment as a block in a global block adjustment algorithm. The technique sought to simultaneously minimize overlap differences from step one and Tycho-2 (available by then) residuals. This had the effect of bringing Tycho-2 information across scan boundaries, greatly benefiting scans with a sub-standard number and/or distribution of reference stars. In the third step the relative frame-to-frame positions from step one were adjusted using the results of step two and locked in place during a reprocessing of the pipeline. This reprocessing incorporated other improvements as well, including distortion correction and the use of Tycho-2 as the reference catalog.
Position reconstruction in the scan processing pipeline was divided into two primary tasks. The first task, accomplished by the Position-of-Frames (PosFrm) module, was the reconstruction of frame positions and the second, accomplished by the Position-of-Points (PosPts) module, was the reconstruction of point source positions. These tasks were well separated in the 2MAPPS pipeline because relative frame positions were required before the multi-frame extractions, profile-fit photometry and band merging could occur. The final reconstructed point source positions, on the other hand, could not be determined until after the multi-frame extractions, profile-fit photometry and band merging had occurred.
i. Reconstruction of Frame Positions
By necessity, PosFrm used single-frame extractions to tie the frames together. In order to minimize random walk, PosFrm simultaneously tied the frames to a set of absolute reference points, even as they were tied together. Thus, PosFrm frame positions were accurate in an absolute as well as relative sense. The absolute reference points were obtained from the U.S. Naval Observatory's ACT Reference Catalog. This catalog (988,758 stars) overcame the short-baseline proper motion limitations of the original Tycho catalog by combining it with the 100-year-baseline Astrographic Catalog.
During the scan of a survey Tile (see III.2a), through a combination of scan rate and secondary mirror motion, the 2MASS telescope would freeze the sky at 273 points along the scan. These are generally referred to as "frames", but herein they will be referred to with all caps as "FRAMES". For each FRAME, point source extractions were available for Read_1 and Read_2-Read_1 for each of the three bands, yielding 6 lower case "frames" consisting of J1, J2, H1, H2, K1 and K2. It was PosFrm's task to bring all the frames together. Since scans were executed by displacing each FRAME one sixth of its width from the last, a single star could show up in six FRAMES (36 frames). In order to be assured of 6-deep FRAME coverage, the offset was made a little less than one sixth of a FRAME width resulting in a small percentage of the scan covered by seven FRAMES (42 frames). The number of frames on which a single true source could appear was quite significant. As will be shown later, it provided a powerful lever for tying the frames together.
PosFrm solved for the frame positions by minimizing a weighted sum of squares of the position differences between multiple frame observations of each common source as well as between frame observations and reference star positions. In order to end up with a set of LINEAR equations the problem was formulated to solve for small differences from a priori parameter estimates. Model parameters for which to solve were chosen to strike a balance between the fidelity of the model and limitations imposed by the minimum number of difference measurements available per scan.
Before proceeding to a more detailed description of PosFrm reconstruction it is first necessary to define some parameters and coordinate systems (see Table I). The first step toward an optimized solution was to express all single-frame extractions and reference stars in a common coordinate system. Since the combined pixels of the three detector arrays involved swept out a narrow (~8.5´ wide) near-great-circle path across the sky, the common system could be Cartesian without any significant loss of accuracy. The system selected is referred to as the Universal scan (U-scan) system which has its origin at the center of the first FRAME and its y-axis running along the common scan path increasing to the north. A set of coordinate transformations were needed to bring the band-frame (B-frame) single-frame extraction positions available into the U-scan system. Discussion of these transformations is below, after additional parameters have been introduced.
Tying the frames to each other and to the sky required knowledge of which frame-level extractions shared a common source and which of those common sources could be matched to reference stars. A priori knowledge of the band-to-band relationships was sufficiently accurate to identify the extractions which share a common source. Matching to reference stars was not as straightforward since a priori knowledge of the absolute position was considerably worse than band-to-band knowledge. To accomplish this a Nominal scan (N-scan) system was defined such that the y-axis points precisely north along the of-date meridian, the x-axis points west and the origin is set by a priori knowledge. It's important to note that, once set, the N-scan system was precisely defined with respect to J2000; thus, no positional accuracy was lost by converting ACT positions to N-scan coordinates. If the a priori knowledge were perfect and the telescope scanned right along the of-date meridian, then the U-scan and N-scan systems would have been coincident. Neither was true, but differences between the two systems were quite small. We were then in position to do a pattern match between the reference stars in N-scan coordinates and the 2MASS extractions in U-scan.
The matching was accomplished using a simple but effective approach referred to as a "two-peg pattern matcher". Two reference stars, well separated in-scan and well away from the scan edges, were selected as the "reference pegs". The task of the matcher was to find the corresponding pair of 2MASS extractions which will be referred to as "extraction pegs". All extractions within an uncertainty radius of each of the reference pegs were candidates for the extraction pegs. The pattern matcher walked through the possible pairs of candidate extraction pegs and performed a linear transformation (2 translation, 1 rotation and 1 scale [in-scan only]) to force the selected candidate extraction pegs to the reference pegs. The attempt was then scored based on how many additional matches resulted from that transformation. For a correct selection of extraction pegs, the additional match count would jump far above the random match level. In the rare event that no pattern match was found among the extraction peg candidates, the algorithm selected new reference pegs and repeated the process. This technique was efficient for several reasons. Extraction peg candidates were prioritized based on magnitude and radial distance from the reference pegs. Once a pattern match was found the search could stop. The absolute pointing of the 2MASS telescopes was excellent, so the a priori positions were usually within about 10´´. Once a pattern match was obtained, a five-parameter linear transformation (2 translation, 1 rotation, 2 scale) was fitted using all 2MASS/reference matches. Using that transformation the reference stars were then placed in the U-scan system.
Given enough extractions, reference stars and computer resources, a five parameter linear fit for each frame would have been ideal. Doing so would have involved solving for five variables per frame (30 variables per FRAME) resulting in 8190 variables for a standard 273 FRAME survey scan. In order to reduce the scope of the problem to a more workable size, a number of carefully chosen simplifying assumptions were made. Those simplifications involved moving some parameters to be solved from frame-level up to scan-level. The simplifications resulted in a parameter set reduced to 546 frame-level and 17 scan-level parameters, for a total of 563. While still large, the resulting set of 563 simultaneous equations proved to provide consistently stable solutions over the wide array of source densities encountered.
Simplifying assumptions included the following:
1) H2 and K2 frame centers differ from J2 centers by constant translational offsets (DxJ2H, DyJ2H, DxJ2K, DyJ2K) over an entire scan, where:
DxJ2H = DxJ2H_0 + dDxJ2H
DyJ2H = DyJ2H_0 + dDyJ2H
DxJ2K = DxJ2K_0 + dDxJ2K
DyJ2K = DyJ2K_0 + dDyJ2K
The parameters ending in "_0" are a priori estimates and the parameters
beginning with "dD" are small adjustments to be solved for, providing
4 of the 17 scan level parameters.
2) Read_1 frame centers differ from Read_2-Read_1 frame centers of the same band by translational offsets (DxR1, DyR1) which vary linearly with frame number:
DxR1 = (mxR1_0 +dmxR1)*nf + (cxR1_0 +dcxR1)
DyR1 = (myR1_0 +dmyR1)*nf + (cyR1_0 +dcyR1)
The parameters ending in "_0" are a priori estimates of the linear
coefficients and those beginning with "dm" and "dc" are small
small adjustments to be solved for, providing an additional 4
scan-level parameters. In these equations "nf" refers to frame number.
3) Rotation angles (TJ, TH, TK), cross-scan scale factors (SXJ, SXH, SXK) and in-scan scale factors (SYJ, SYH, SYK) of individual frames remain constant within each band over the entire scan.
TJ = TJ_0 + dTJ
TH = TH_0 + dTH
TK = TK_0 + dTK
SXJ = (1 + dSXJ)*SXJ_0
SXH = (1 + dSXH)*SXH_0
SXK = (1 + dSXK)*SXK_0
SYJ = (1 + dSYJ)*SYJ_0
SYH = (1 + dSYH)*SYH_0
SYK = (1 + dSYK)*SYK_0
Parameters beginning with "T" are rotation angles and those
beginning with "dT" are small rotation angle adjustments to be
solved for. Those beginning with "SX" and "SY" are cross-scan and
in-scan scale factors, respectively. As before, the parameters
ending in "_0" are a priori estimates. The parameters beginning with
"dS" are small adjustments to be solved. Taken together these
provide the remaining 9 scan-level parameters
In addition to the 17 scan-level parameters, there remained 546 frame-level parameters in a standard survey scan. Those were the two translational adjustments (dxJ2n,dyJ2n) associated with each of the 273 J2 frame centers.
Table II lays out the equations
needed to convert from B-frame to U-scan coordinates. The equations include
all the small adjustment variables for which we would like to solve. Define
"S" to be the sum of weighted differences squared for all combinations of
all extractions associated with a common source
regardless of type (J1, J2, H1, H2, K1, K2) or FRAME number. Add into
"S" the weighted differences squared between each matched reference star
and every extraction to which it can be matched. Note that since every
extraction is differenced from every other extraction of a common source
the number of measurements goes up very rapidly.
Finally add into "S"
the sum of very lightly weighted differences squared where the differences
are in fact changes with respect to the a priori frame-to-frame positions.
This is added
to handle an extreme case where no common source extractions exist to
tie in one or more frames. The weighting is set low enough that it has
no effect on the solution under normal circumstances.
Take the partial derivative
of "S" with respect to each of the 563 adjustment variables previously discussed
and set to zero. This results in a large set of simultaneous linear
equations which can then solved for the desired variables.
The process just described is presented mathematically in
Table III.
The partials were setup to be solved symbolically using MAPLE
(Maple V Release 3 for MS Windows by Waterloo Maple Software and
the University of Waterloo), which was
directed to output Fortran code. Note that the form of the partial varies
with the terms within the summation depending on the combination of types being
differenced (J1:J1, J1:J2, J1:H1, J1:H2...) as well as for each combination
of type vs. reference star (J1:RS, J2:RS, H1:RS,...). Each combination was
fed to MAPLE and the code output by Maple was then modified
by a routine written specifically for the purpose to make it compatible
with the rest of PosFrm. This process resulted in a number of Fortran routines
consisting of thousands of lines of machine generated code.
The routines were thoroughly tested and proved to work very well.
After all the small adjustments had been determined, they were used
in the coordinate conversion equations from
Table II to obtain U-scan positions for
all the frame-level extractions used in the reconstruction. These
data were used to verify that all six frame types had been brought
successfully together over the entire scan. All extractions associated
with a common source (up to 42 extractions/source) were merged together
to generate the PosFrm Merged Point (PFMP) file. The merged point positions
were also transformed from U-scan through N-scan to J2000 and these positions
were carried in the PFMP file as well. Differences between
the PFMP and ACT positions were monitored during processing for quality
assurance.
Well after the aforementioned least-square equations were derived, coded
and tested, it was discovered that the relative band-to-band positions
could sometimes change by small amounts during the course of a single
scan due to flexure in the camera or small motions of the arrays themselves.
Modeling the band differences as linear with frame number, rather than
constant, appeared a better way to go. Rather than go back to rederive,
recode and retest, with associated time delays and risks, it was decided
to add a separate linear fit for each band to minimize differences
with respect to the PFMP positions obtained from the original solution.
ii. Reconstruction of Point Source Positions
After the Atlas Images were assembled using the frame positions as determined
by PosFrm, point sources were detected from the Atlas Images and extracted using
all available multi-frame, multi-band information. The resulting
bandmerged sources were matched to the PFMP sources previously generated by
PosFrm and already tied to
the ACT. Using points in common between the two sets of merged sources,
PosPts performed a single five-parameter linear fit to remove
any biases which might have resulted from the two different extraction methods.
After preliminary pipeline processing of all scans, a good deal of
additional information useful to position refinement became available. This
information came in the form of position differences of sources common to
overlapping scans. In order to address systematic errors over the
scan length arising from random walk, each scan was divided into 12
half degree long segments.
Trimmed means were computed separately
in cross-scan and in-scan for each segment with respect to all overlapping segments
from other scans. The problem was then to find the best cross-scan and
in-scan adjustments for each scan segment in order to simultaneously
minimize overlap differences and Tycho-2 residuals globally.
In addition, it was found that allowing the
cross-scan scale factor to be fitted as well improved results.
One of the biggest challenges to determining the block adjustments
was the sheer size of the problem. Although the catalog would ultimately
contain 59731 scans, adjustments were needed for 70744 candidate scans.
Each scan had 12 segments and each segment had 2 or more (often many more)
overlapping segments from other scans. In order to keep the problem
manageable the sky was broken down into 5 overlapping zones. Zone A
included Dec bands 1-9, Zone B bands 8-14, Zone C bands 13-18,
Zone D bands 17-23 and Zone E bands 22-30. Each zone was solved
separately and then combined with the others after discarding the extra
Dec band from each zone.
The algorithm used will be discussed in more detail in subsection iii.
Before that two other items need to be addressed.
i. Removing Distortion
In order to avoid introducing biases, distortion had to be removed before
the overlap differences were computed.
It would have been best to remove it at the band frame level
during the preliminary pipeline processing. Unfortunately circumstances
prevented putting band-frame distortion correction in place prior to start of processing.
Fortunately it proved possible to
remove most of the distortion after preliminary processing
using bandmerged positions.
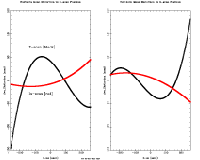
Based on a very large number of USNOA residuals from
calibration scans in the preliminary pipeline processing mean in-scan (red)
and cross-scan (black) bandmerged distortion errors were determined
as a function of cross-scan position (X_us) and are plotted in
Figure 1. These mean distortions were then
subtracted from the preliminary positions before the overlap differences were
computed. See VI.6c for an analysis of the
band-frame distortion correction.
Solving for Adjustments
b. Global Block Adjustments
 |
| Figure 1 |
ii. Generating Segment Weighting Factors
In order to serve as weighting factors for segment adjustments a set of pre-adjustment variances were iteratively determined. Initially all segments were assigned a nominal variance (V0). The iterations were used to determine the variance factor (vf) for each segment which would drive the mean of the overlap chi-squares to one. For each overlap the variance factor for segment "i" as indicated by its overlap with segment "j" (vf_ij) was computed as
vf_ij = (1/V0)*(dx_ij)*(dx_ij) - vf_j
where "dx_ij" is the overlap difference between segments "i" and "j" and "vf_j" is the variance for segment "j". In order to prevent a single bad segment from unduly raising the variances of its neighbors the variance factor for a segment was not immediately set to the average (vfave) indicated by all its overlaps. Instead it was initially set to the minimum (vfmin) indicated by all its overlaps. With each succeeding iteration it was moved a little closer to the average.
vf = vfmin + alpha*(vfave-vfmin), where alpha = (it-1)/(itmx-1)
and "it" is the iteration number and "itmx" the maximum number of iterations. All the variance factors were initially set to 1.0 and were never allowed to fall below a small positive number. After the variance factors were thus determined the corresponding variances were computed (V_i=V0*vf_i).
iii. Obtaining Segment Adjustments
The segment adjustments were also generated iteratively. The algorithm considered information from three different sources in making each adjustment decision. First came the inverse variance weighted mean of the overlap differences. Next came the inverse variance weighted Tycho-2 differences. Note that this is a super set of the ACT available to the preliminary pipeline processing. Finally came the segment-to-segment differences for same scan segments. The intent was to minimize the same-scan segment-to-segment differences simultaneously with the overlap and Tycho-2 differences. For each segment, in each iteration, a change in in-scan and cross-scan segment adjustment was computed independently as a weighted sum of the three sets of differences. Only a fraction of that computed change was then taken. That fraction increased linearly with iteration step up to a value of 1.0. At each iteration step changes to the cross-scan scale factor were made in a similar manner and then factored back in to the overlap differences on the next step.
Once the segment adjustments were determined a set of post-adjustment segment uncertainties were generated via the method described previously for the pre-adjustment uncertainties.
The pipeline reprocessing was done in a similar manner to the preliminary processing, but with some significant changes. The a priori frame positions came from the preliminary pipeline results modified using the segment adjustments just described, with frame adjustments linearly interpolated between segment centers. Relative J-band frame positions were locked in place and the reconstruction algorithm was not allowed to change them. Distortion corrections as a function of x:y position within the frame were implemented separately for the three bands in both hemispheres. The reference catalog was changed from the ACT to Tycho-2.
After reprocessing, analysis showed a relatively small set of scans (987/59731 => 1.65%) for which quoted uncertainties did not appear to adequately reflect the errors over a portion of the scan. As a result uncertainty adjustments were made to portions of the 987 scans. The uncertainty adjustments touched a total of 0.56% of the catalog sources. The 987 scans affected are listed in Table 4. These adjustments are reflected in the All-Sky Catalog,
[Last updated: 2003 March 03; by H. McCallon and R. Cutri]