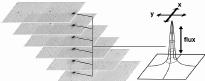
The primary photometry and position estimation algorithm for each candidate detection from the Atlas Images is point source profile-fitting. This provides the most robust estimation for faint sources and objects in denser or more complex environments. Although the detection is done on the coadded Atlas Images, the point source fit is performed directly on the flat-fielded pixel values in a stack of 6 frames, using knowledge of the PSF shape and the relative position offsets for the frames. The latter have already been determined during the Atlas Image generation (cf. IV.3). This is illustrated in Figure 1; the position and amplitude of the source profile is determined during the fitting procedure, but the relative positions of the frames in the stack are held fixed.
 |
| Figure 1 |
We now discuss the mathematical details of the procedure used.
PSF-fitting photometry is based on the data in the neighborhood of each
candidate detection, as defined by a ``data circle'' of radius 2 pixels,
centered on the nominal location of the detection. We start by
writing a measurement model which expresses
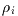 the observed pixel value corresponding to the ith point within the
data circle, in terms of the quantities that we wish to estimate.
For an isolated object, i.e.,
one which is sufficiently distant from its neighbors that there is no
interaction between the corresponding PSFs, these
quantities consist simply of the flux and position of the object.
However, if the point source detection algorithm reports multiple candidates
closer than approximately 5´´ (the precise number varies with the
actual seeing), then the profiles will be fit to each detection simultaneously.
The number of sources being solved for simulaneously is referred to as
the blend number, NB.
the observed pixel value corresponding to the ith point within the
data circle, in terms of the quantities that we wish to estimate.
For an isolated object, i.e.,
one which is sufficiently distant from its neighbors that there is no
interaction between the corresponding PSFs, these
quantities consist simply of the flux and position of the object.
However, if the point source detection algorithm reports multiple candidates
closer than approximately 5´´ (the precise number varies with the
actual seeing), then the profiles will be fit to each detection simultaneously.
The number of sources being solved for simulaneously is referred to as
the blend number, NB.
A suitable measurement model is then:
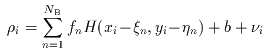 |
 |
(Eq. IV.4.b.1) |
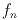 ,
,
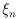 ,
and
,
and 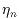 represent the flux and (x,y) location of the nth source in the
blend; (xi,yi) represents the angular position
in the sky corresponding to the ith pixel (obtained from the focal-plane
position and dithering offsets), H(x,y) is the point
spread response (PSF), b is the local background (estimated separately),
and
represent the flux and (x,y) location of the nth source in the
blend; (xi,yi) represents the angular position
in the sky corresponding to the ith pixel (obtained from the focal-plane
position and dithering offsets), H(x,y) is the point
spread response (PSF), b is the local background (estimated separately),
and 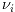 represents
the measurement noise. The latter is modeled as a zero-mean Gaussian random
process whose covariance can be expressed as:
represents
the measurement noise. The latter is modeled as a zero-mean Gaussian random
process whose covariance can be expressed as: |
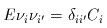 |
(Eq. IV.4.b.2) |
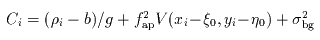 |
 |
(Eq. IV.4.b.3) |
 is the background noise [dn] representing the combined
effects of Poission noise, read noise, and confusion, estimated
from the standard deviation of pixel values in an annulus
surrounding the source (see Table 1 for a time history of the pixel gain and
read noise values).
Also in the above equation,
fap is the estimated flux density from aperture photometry,
V(x,y) is the PSF variance at offset (x,y) from center
(calculated during the PSF estimation procedure), and
is the background noise [dn] representing the combined
effects of Poission noise, read noise, and confusion, estimated
from the standard deviation of pixel values in an annulus
surrounding the source (see Table 1 for a time history of the pixel gain and
read noise values).
Also in the above equation,
fap is the estimated flux density from aperture photometry,
V(x,y) is the PSF variance at offset (x,y) from center
(calculated during the PSF estimation procedure), and
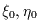 represent the nominal position of the candidate detection.
The error associated with using the nominal rather than true source position
is incorporated in V(x,y). The dominant term in the noise model depends
on the source flux. For the brightest sources (J < 12), the dominant term is
PSF error (2nd term on the right hand side of Eq. IV.4.b.3); the
faintest sources (J > 15) are dominated by the background term, corresponding
to the last term on the right hand side of the equation.
represent the nominal position of the candidate detection.
The error associated with using the nominal rather than true source position
is incorporated in V(x,y). The dominant term in the noise model depends
on the source flux. For the brightest sources (J < 12), the dominant term is
PSF error (2nd term on the right hand side of Eq. IV.4.b.3); the
faintest sources (J > 15) are dominated by the background term, corresponding
to the last term on the right hand side of the equation.
|
Table 1: Time history of pixel gain and read noise values
| |||||||
| Pixel gain [electrons/dn] |
Read noise [electrons] | Hemisphere | Date Range | J | H | Ks | J | H | Ks |
| North | 05/21/1997 - 06/04/1998 | 10.0 | 10.0 | 8.0 | 40.0 | 40.0 | 56.0 |
| 06/05/1998 - 09/16/1998 | 10.0 | 10.0 | 8.0 | 42.0 | 40.0 | 57.0 | |
| 09/19/1998 - 10/23/1998 | 10.0 | 10.0 | 8.0 | 42.0 | 40.0 | 57.0 | |
| 10/24/1998 - 07/23/1999 | 10.0 | 8.0 | 6.5 | 44.0 | 50.0 | 54.0 | |
| 09/13/1999 - end | 7.9 | 9.4 | 8.7 | 38.0 | 42.0 | 44.0 | |
| South | 03/18/1998 - 02/26/1999 | 8.5 | 8.0 | 9.9 | 43.0 | 45.0 | 45.0 |
| 03/01/1999 - end | 6.8 | 7.7 | 10.0 | 45.0 | 41.0 | 50.0 | |
The goal of the estimation procedure is to obtain the most probable values
of the quantities  ,
,
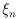 ,
,
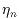 (where n = 1,...,
NB).
To simplify the notation, we will form a vector, z, of unknowns,
whereby the components of z are:
(where n = 1,...,
NB).
To simplify the notation, we will form a vector, z, of unknowns,
whereby the components of z are:
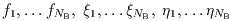 .
Also, we will use
.
Also, we will use 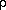 to denote the
vector whose components are
to denote the
vector whose components are
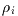 :
i=1,...,M, where M is the number
of pixel values within the data circle. Our goal can then be expressed in
terms of obtaining the most probable value of z
(denoted
:
i=1,...,M, where M is the number
of pixel values within the data circle. Our goal can then be expressed in
terms of obtaining the most probable value of z
(denoted 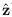 ) conditioned on
) conditioned on
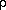 ,
i.e., to maximize the conditional probability
,
i.e., to maximize the conditional probability
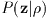 .
If we have no information a priori on the distributions of possible
values of the components of z, then it is appropriate to regard the
a priori probability density distribution of z as flat,
i.e., P(z)= constant. In this case, Bayes' rule tells us that
the most probable value of z can be obtained equally well by maximizing
.
If we have no information a priori on the distributions of possible
values of the components of z, then it is appropriate to regard the
a priori probability density distribution of z as flat,
i.e., P(z)= constant. In this case, Bayes' rule tells us that
the most probable value of z can be obtained equally well by maximizing
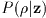 , since it differs from
, since it differs from
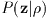 only by an
ignorable constant. This is known as the maximum likelihood procedure, and
is the procedure used in the 2MASS profile fitting photometry. Since the
measurement noise is assumed to be Gaussian, we can write an expression for
only by an
ignorable constant. This is known as the maximum likelihood procedure, and
is the procedure used in the 2MASS profile fitting photometry. Since the
measurement noise is assumed to be Gaussian, we can write an expression for
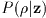 as follows:
as follows:
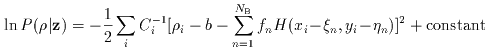 |
 |
(Eq. IV.4.b.4) |
The maximization of this expression with respect to z is
actually performed as a minimization of
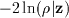 , using the conjugate
gradient method.
, using the conjugate
gradient method.
The next step is to examine the goodness of fit to the data, which is
accomplished by calculating the reduced 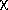 2,
given by:
2,
given by:
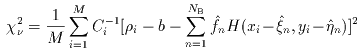 |
 |
(Eq. IV.4.b.5) |
If the solution represents a reasonable fit to the data, then
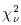 ~1. Otherwise, we would
conclude that
the model involving NB sources is inadequate, which could be
due either to an extended source or a close blend of point sources.
No attempt is made to deconvolve
single candidates with poor profile fits (i.e., large
~1. Otherwise, we would
conclude that
the model involving NB sources is inadequate, which could be
due either to an extended source or a close blend of point sources.
No attempt is made to deconvolve
single candidates with poor profile fits (i.e., large
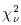 values).
values).
The uncertainties of the estimated quantities can be obtained from the
curvature of ln 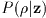 , as
discussed by Whalen (1971, ``Detection of Signals in Noise," Academic Press,
New York). Specifically, we define a matrix
, as
discussed by Whalen (1971, ``Detection of Signals in Noise," Academic Press,
New York). Specifically, we define a matrix 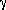 as
follows:
as
follows:
 |
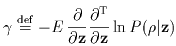 |
(Eq. IV.4.b.6) |
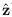 .
.
>From Eqs. IV.4.b.4 and IV.4.b.6, the individual components of
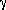 are given by:
are given by:
 |
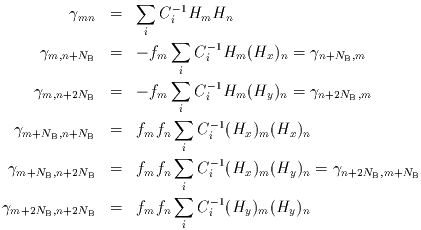 |
(Eq. IV.4.b.7-12) |
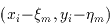 , and
(Hx)m,
(Hy)m denote the corresponding quantities
obtained from partial derivatives of H(x,y) with respect to its two
arguments, respectively.
, and
(Hx)m,
(Hy)m denote the corresponding quantities
obtained from partial derivatives of H(x,y) with respect to its two
arguments, respectively.
The diagonal elements of the inverse of 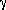 then
correspond to lower limits for the variances of the estimated quantities,
i.e.,
then
correspond to lower limits for the variances of the estimated quantities,
i.e.,
 |
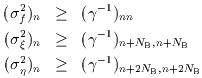 |
(Eq. IV.4.b.13 - 15) |
It can be shown that if the measurement model is linear, equality holds in the above expressions, but otherwise the derived variances represent lower limits only. In practice, the measurement model is sufficiently linear in the neighborhood of the solution that these quantities are truly representative of the respective uncertainties.
In cases for which
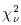 is large (>2), the quoted
flux uncertainty may not accurately reflect the true uncertainty since a poor
profile fit indicates a violation of the statistical assumptions associated
with the measurement model. There is, in fact, no direct correlation between
the
is large (>2), the quoted
flux uncertainty may not accurately reflect the true uncertainty since a poor
profile fit indicates a violation of the statistical assumptions associated
with the measurement model. There is, in fact, no direct correlation between
the 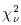 values and the quoted
uncertainties since the latter are determined from an a priori
error model (albeit with some data-dependent parameters) which does not
incorporate the a posteriori information regarding the quality
of the fit. In most cases, a large value of
values and the quoted
uncertainties since the latter are determined from an a priori
error model (albeit with some data-dependent parameters) which does not
incorporate the a posteriori information regarding the quality
of the fit. In most cases, a large value of
 would indicate the
presence of confusion. This is borne out by scatter plots of the magnitude
difference (PSF - aperture) as a function of
would indicate the
presence of confusion. This is borne out by scatter plots of the magnitude
difference (PSF - aperture) as a function of
 , an example of which
is shown in
Figure 2, made using all sources brighter
than 11th magnitude at J, H, and K in a region of radius 1 degree in
Baade's Window. This figure, in which the magnitude difference has been
expressed in units of
, an example of which
is shown in
Figure 2, made using all sources brighter
than 11th magnitude at J, H, and K in a region of radius 1 degree in
Baade's Window. This figure, in which the magnitude difference has been
expressed in units of
 = (
= ( PSF2 +
PSF2 +  ap2)1/2
(where
ap2)1/2
(where
 PSF and
PSF and
 ap
represent the errors associated with PSF-fitting and aperture photometry,
respectively), shows the expected trend in which the magnitude difference
increases with
ap
represent the errors associated with PSF-fitting and aperture photometry,
respectively), shows the expected trend in which the magnitude difference
increases with
 , due to the increasing
amount of confusion flux in the standard aperture.
, due to the increasing
amount of confusion flux in the standard aperture.
 |
| Figure 2 |
Correction to Photometric Errors
The validity of the calculated flux uncertainties can be checked by comparing
them with the repeatability of the estimated flux for a given source
for which multiple observations are available. Suitable data for this purpose
are the calibration scans, made frequently each night in sets of 6
observations of the same region. Using such data, the flux repeatability
has been compared with the uncertainties calculated from Eq. IV.4.b.13.
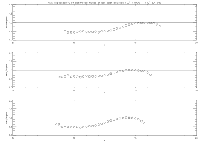
Figure 3 shows a representative set of
results in which the RMS repeatability, expressed in units of the
calculated sigma, has been plotted as a function of magnitude.
 |
| Figure 3 |
It is apparent from Figure 3 that the calculated error has been systematically
overestimated by about a factor of 2 for the brighter sources (J < 14).
This problem has been traced to
the estimated PSF variance, V(x,y), which was found to be dominated by
a spurious systematic component which arose during the PSF estimation
process. This component was related to the errors of sinc interpolation
onto an undersampled grid, necessitated by limitations of computational
processing time. The problem was rectified after the initial processing
by subtracting in quadrature from the derived flux errors
(in magnitudes) a correction term,
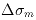 ,
obtained in a semi-empirical manner by comparing the RMS repeatability with
the calculated uncertainty for a large representative sample
of calibration stars. Although it can be
shown that the resulting correction term
is magnitude-independent to a good approximation, its value does
depend on the details of the PSF used in the photometric
parameter estimation. Therefore, a correction value was
estimated individually for each member of the PSF library, except for those
cases in which too little data were available to obtain good repeatability
statistics. For the latter PSFs, the adopted values of
,
obtained in a semi-empirical manner by comparing the RMS repeatability with
the calculated uncertainty for a large representative sample
of calibration stars. Although it can be
shown that the resulting correction term
is magnitude-independent to a good approximation, its value does
depend on the details of the PSF used in the photometric
parameter estimation. Therefore, a correction value was
estimated individually for each member of the PSF library, except for those
cases in which too little data were available to obtain good repeatability
statistics. For the latter PSFs, the adopted values of
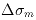 were obtained from the
set of valid solutions via
power-law extrapolation with respect to the seeing index.
The complete set of
were obtained from the
set of valid solutions via
power-law extrapolation with respect to the seeing index.
The complete set of
 values may be accessed
via Table 2.
Also listed in this table are the corresponding "floor" values,
values may be accessed
via Table 2.
Also listed in this table are the corresponding "floor" values,
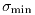 ,
representing the minimum permitted values of the corrected flux
uncertainties. The floor was
necessitated by the fact that the uncorrected sigma is a stochastic quantity
whose distribution is of finite width, which would otherwise lead to occasional
instances in which the quadrature subtraction of
,
representing the minimum permitted values of the corrected flux
uncertainties. The floor was
necessitated by the fact that the uncorrected sigma is a stochastic quantity
whose distribution is of finite width, which would otherwise lead to occasional
instances in which the quadrature subtraction of
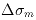 produced an anomalously
low result.
produced an anomalously
low result.
Based on the above considerations, the corrected uncertainty of
the estimated flux in magnitudes,
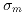 is then given by:
is then given by:
 |
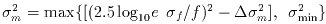 |
(Eq. IV.4.b.16) |
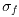 is the uncorrected
flux uncertainty given by Eq. IV.4.b.13.
is the uncorrected
flux uncertainty given by Eq. IV.4.b.13.
Representative plots of the calculated flux uncertainty as a function of magnitude both before and after the correction, generated from calibration scan data, are shown in Figure 4.
Additional sources of error
In addition to the error sources allowed for explicitly in the error model represented by Eq.IV.4.b.3, the "combined" photometric uncertainties quoted in the Point Source Catalog ([jhk]_msigcom parameter) include the effects of flat fielding error and the uncertainty of absolute calibration, both of which are ~ 0.01 mag. Various other potential sources of error have been investigated, and they include:
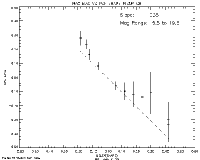
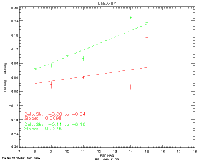
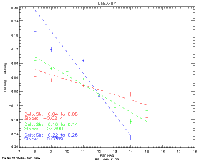
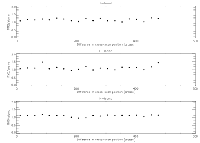
(1) PSF shape mismatch due to seeing variations: During the photometric solution procedure, the assumed form of the PSF was obtained from table lookup with respect to a dimensionless "seeing index," a quantity which was updated at regular time intervals during each survey scan, and which took values typically in the range 0.9 (excellent seeing) to 1.3 (poor seeing). The problem is that seeing variations between updates could result in a mismatch between the assumed PSF and its true instantaneous value. Similarly, seeing variations during the data scans used to construct the PSFs themselves could result in a mismatch between the nominal and true seeing index associated with a given PSF. The effect of PSF seeing mismatches has been investigated using numerical experiments in which subsets of 2MASS data were analyzed photometrically using PSFs deliberately based on the wrong values of seeing index. The results showed a magnitude bias which depended on the offset of the perturbed seeing index from its true (base) value. Typically, the magnitude bias was roughly proportional to the offset in seeing index, as illustrated by Figure 5, which shows a plot of the magnitude bias (represented by the difference between the PSF and aperture magnitudes, without any correction being applied for PSF/aperture normalization) and the offset in the seeing index (the difference between the seeing index associated with the selected PSF and the true value, the latter being 1.076 in this case), averaged over all magnitudes at K-band. It was also found that the effect decreased with increasing source flux (due to the magnitude-dependent weighting of the PSF in the photometry solution). This is illustrated by plots of the magnitude bias as a function of magnitude for various offsets of the seeing index, as exemplified by the K-band data shown in Figure 6 (offset < 0), Figure 7 (offset = 0), and Figure 8 (offset > 0). As before, no correction was applied for PSF/aperture normalization. The values of magnitude bias presented in Figures 6 and 8 are substantially greater than those which would be expected in the survey data since large offsets in seeing index were used in the numerical experiments. Specifically, since typical mismatches of the seeing index were of the order of the PSF bin sizes (0.02), the expected magnitude biases would be of this same order. Also, since the effect is greatest for the faintest sources which have the largest flux errors, we conclude that the effect on the quoted uncertainty of an individual source would probably not be significant. There would, however, be noticeable deviations from photometric linearity when the results of a large number of sources are averaged. Similarly, systematic biases at the few-percent level in both color and magnitude could be expected over patches of sky which share a common mismatched PSF.
PSF mismatches can also occur as a result of the finite width of the PSF bins with respect to the seeing index, depending on where the actual seeing value falls in relation to the boundaries of the particular bin. For a typical bin size of 0.02, the result would be a uniformly-distributed random error of ±0.01 mag, whose effects would be similar to those of seeing-induced mismatches.
|
|

|
|
| Figure 5 | Figure 6 | Figure 7 | Figure 8 |
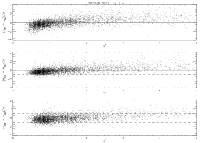
(2) PSF shape mismatch due to optical distortions which vary with focal-plane position: The systematic variation of the PSF across the focal plane would, if uncorrected, produce a corresponding position-dependent magnitude bias. Fortunately, in the in-scan direction, the effect is effectively averaged out as a result of the fact that each source is observed at 6 evenly-spaced in-scan locations along the focal plane. For the cross-scan variation, however, an empirically-determined post facto correction has been applied to the photometry. As a check on the validity of this correction, the flux repeatability has been investigated for observations of a given source at different cross-scan positions on the focal plane, by making plots of RMS repeatability as a function of the difference in cross-scan position. An example is shown in Figure 9, made using survey data from a 6 degree square region in the vicinity of Baade's Window; the RMS repeatability has been expressed in units of the calculated uncertainty, sigma. The results indicate that, after having applied the cross-scan bias correction, there is no significant residual bias in the photometry across the focal plane.
 |
| Figure 9 |
(3) PSF/aperture normalization: The errors associated with this factor are discussed in subsection (i) of Section 4c, "Photometric Normalization."
Comments on deblending
The blend number, NB is specified in each record of the
Point Source Catalog as "bl_flg" (blend flag), and
indicates the number of candidates fit simultaneously. Blend
flag values >1 are therefore useful as indicators of possible confusion in
regions of high source density. For example,
Figure 10 shows the Ks image of sources 2MASSI J0009220+343350
and 2MASSI J0009260+335945. The former is the brighter of the two
objects, and is a 3-band detection having a bl_flg of "112." The
latter source is the fainter of the pair, is detected only in the H and
Ks bands, and has a bl_flg of "012." Both sources
are clearly visible in all three bands, but the pair was resolved only
in H and Ks. The separation of the pair in Ks
was small enough so that the profile fitting was run simultaneously
on both sources (NB=2), but in H the separation was large
enough that the sources were fitting individually. The
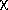 2
value of the J-fit in the bright source is 6.35, indicating that
the single PSF-fit was poor.
2
value of the J-fit in the bright source is 6.35, indicating that
the single PSF-fit was poor.
Objects with valid profile-fit Read_2-Read_1 photometry (i.e., non-saturated and converged profile fit) have ``rd_flg'' values of ``2'' in the Point Source Catalog record. This corresponds to the great majority of all point sources in the Catalog.
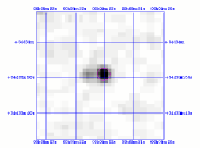 |
| Figure 10 |
Point Spread Functions and Seeing Estimation
The source contribution to the profile fit model is proportional to a point-spread-function (PSF) which was taken from a library of PSFs indexed by seeing for each band. PSFs were not derived "on-the-fly" during 2MASS pipeline processing because of the difficulty in automated PSF construction in much of the sky due to both very low and very high source density. PSF derivation is itself a cpu-intensive task, so the use of a PSF library resulted in much faster processing run times. Each PSF in the library was regarded as isoplanatic for the purpose of the data processing.
The library PSFs corresponding to specific seeing values were constructed empirically using data from single 2MASS calibration scans (cf III.2.c) having that average seeing value. Selection of the calibration scans was based on criteria such as small variability of the seeing parameter during the scan, and the x- and y- central moments of the stars being equal (typically within 10%). Images of the 50 brightest stars in each scan were then obtained on sampling grids of interval 0.5 pixels in each axis using a linear estimator designed to produce the most probable estimate based on a Gaussian a priori statistical model of possible images. Each such image was centroided, co-aligned and summed, and the result was sinc-interpolated onto a 1/24-pixel (0.083´´) grid. During the image combination process, each stellar image was examined for consistency with others taken under similar conditions, and the outliers excluded from the sum.
The uncertainty associated with the calculated PSF, in the form of a "variance map," was derived from the residuals with respect to the data pixel values. This map, corresponding to V(x,y) in Eq. IV.4.b.3, was expressed on the same spatial grid as for the PSF and used by the profile fit analysis to estimate the total uncertainties in the resulting estimates.
The above procedure yielded typically 10-20 PSFs within a given seeing bin. To further increase accuracy, each such set of PSFs (and their associated variance maps) was subsequently combined. As before, outliers were excluded based on lack of consistency with other PSFs within the seeing bin.
The PSF generation procedure involved a certain amount of compromise between
accuracy and
processing speed. In particular, some information was lost in the sinc
interpolation step as a result of the fact that the sampling interval for
the individual star images (0.5 pixels) was considerably coarser than the
Nyquist interval of 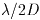 ,
which was approximately 0.05 pixels at the
shortest wavelength. Since the processing speed is roughly inversely
proportional to the fourth power of the sampling interval, a Nyquist sampling
grid would not have been computationally feasible.
,
which was approximately 0.05 pixels at the
shortest wavelength. Since the processing speed is roughly inversely
proportional to the fourth power of the sampling interval, a Nyquist sampling
grid would not have been computationally feasible.
As an illustration of the interpolation error, Figure 11 shows the results of a numerical simulation in which a synthetic PSF has been coarsely sampled and then reinterpolated. The synthetic PSF, shown by the solid line in the upper plot, represents the response of a uniformly illuminated aperture of diameter 1.3 m with 0.23 m central obscuration, convolved with a 2MASS pixel and a Gaussian smoothing function (FWHM = 0.3 pixels) designed to approximate the effect of seeing. This curve has been sampled at intervals of 0.5 and 0.25 pixels and then sinc interpolated to produce the dashed and dotted lines, respectively. The corresponding interpolation errors (interpolated - true) are shown in the lower plot by the dashed and dotted lines, respectively. For comparison, the solid line in the lower plot shows the standard deviation of PSF values (square root of the variance map) for a typical J-band PSF of seeing index approximately 1.0. The plot illustrates that the systematic error in the PSF due to interpolation effects can dominate the variance map.
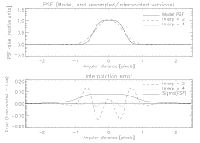
|
| Figure 11 |
If no allowance were made for interpolation error, two undesirable effects would result:
(1) Photometric nonlinearity in which the photometric error (in magnitudes) varies with the source magnitude. This is due to the fact that in the photometric solution procedure, the relative spatial weighting of different parts of the PSF depends on the source flux (see Eqs. IV.4.b.3 and IV.4.b.4).
(2) Overestimation of the errors in source flux, due to the fact that the systematic error is taken out during calibration and should not be included with the stochastic errors. This problem was rectified after the main processing by subtracting (in quadrature) a correction term from the estimated magnitude errors, as discussed above.
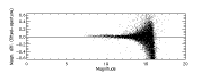
With regard to item (1), Figure 12a illustrates the nonlinearity in estimated flux at J-band resulting from the sinc interpolation of a PSF with a sampling interval of 0.5 pixels. The vertical scale in this plot represents the difference between profile-fit photometry and aperture photometry. For comparison, Figure 12b shows the result of using a pre-interpolation sampling interval of 0.25 pixels. The PSFs corresponding to these two cases are shown in Figure 13.
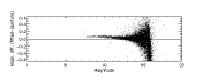
| 
|
| Figure 12a | Figure 12b |
|
| Figure 13 |
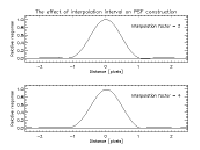
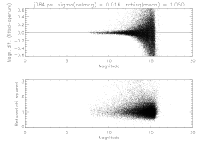
Since the true PSF in the above example is unknown, we cannot reliably evaluate the interpolation error. However, one aspect of the interpolation error that is apparent is the Helmholtz ringing, corresponding to the sidelobes on either side of the main peak of the PSF. Figure 13 shows that the effect is more severe with the coarser sampling interval of 0.5 pixels. It was found that the contamination of the wings of the PSF by this Helmholtz ringing was a significant contributor to the nonlinearity effects in flux estimation, and that the linearity could be improved substantially by truncating the PSF just inside the first sidelobe. The improvement in photometric linearity resulting from the PSF truncation is illustrated by plots of the magnitude delta (difference between profile-fit and aperture magnitudes) as a function of magnitude for Scan 84 on 9/28/1999 at J-band. Figures 14a and 14b show the result of using untruncated and truncated PSFs, respectively. The truncated versions of the PSFs were therefore used in the profile fitting photometry.
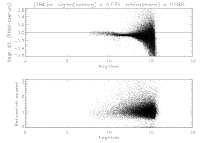
| 
|
| Figure 14a | Figure 14b |
The appropriate PSF was chosen for the profile fitting photometry during the processing of a 2MASS survey scan by estimating the mean point source diameter (seeing) on spatial scales no finer than the length of an Atlas Image, 17´, corresponding to a time interval in the scan of approximately 18 sec. The actual interval used to determine the seeing was driven by source density, and in low star density regions the interval was up to 3 times longer. If the seeing were variable on timescales shorter than the seeing estimation response time, there could have been a photometric error of up to several percent induced by a mismatch between the true image profile and the PSF used in profile-fitting photometry, as discussed above.
[Last Updated: 2003 Mar 13; by R. Cutri & K. Marsh]