IV. 2MASS Data Processing
3. Atlas Image Generation
The reduced R2-R1 frames for each 6°-long scan are spatially registered
and combined into a series of 8.53´×17.07´
(512×1024 pixel, 1´´ per pixel) Atlas Images. The Atlas Images
represent the coaddition of all six overlapping frames as described below. The
images are centered on the cross-scan coverage, and adjacent images within a
scan overlap in declination by 54´´. The J, H, and Ks
band images are produced separately, but are registered onto a common
astrometric grid to facilitate three-color investigations. Atlas Images are
written in FITS format, and contain both the astrometric solution for the
image in the J2000 coordinate system and the nightly calibrated photometric
zeropoints within the FITS header (keyword "MAGZP"). Due to space limitations,
the Atlas Images provided in the release data have been compressed using a
lossy compression algorithm
(hcompress).
The Atlas Images are produced by first spatially registering the
dark-subtracted, flattened, and sky-offset subtracted R2-R1 frames relative to
each other, using the estimated positions of point sources in the frames
(cf. IV.6).
These frames are placed on the output Atlas Image coordinate grid one at
a time, using a flux preserving interpolation kernel (see below). An example
of a portion of a single frame along with the corresponding section of the
combined Atlas Image is shown in Figure 1.
Camera pixels which have
poor responsivities, are excessively noisy, or are affected by transient
effects, such as cosmic rays (as identified by unconfirmed single frame
detections), are masked off during the interpolation procedure. Prior to
adding the frame to the output image, the frame background is adjusted
to match that of those frames already combined into the image, by removing
the median of the differences at each point in the sky in the overlap region
between the incoming frame and the previously-combined frames. This process
produces seamless images, except in cases where the background levels vary
rapidly with time due to clouds, atmospheric OH emission, or severe optical
effects from extremely bright objects (such as beta Pegasi). The final
output Atlas Image represents at each pixel the average of six such
interpolated, background-adjusted frames. Because some pixels are masked,
and there is some margin in the frame overlap, any one pixel in the Atlas
Image may represent the average of anywhere from zero to seven frames.
Output pixels consisting of zero or one frame are set to zero in the
compressed Atlas Images.
Image Estimation Using Kernel Smoothing
The ideal image coaddition represents the best possible estimate of flux
on the sky. Based on well-understood principles from density estimation
{e.g., Density Estimation, B.W. Silverman 1986}, we smooth our square
pixels to remove bias, but not so much that we introduce a large variance
from the original images. The optimal smoothing balances these two sources of
error.
To derive a smoothing formula, we make the minimum knowledge assumption
that a photon hits any point on the pixel with equal probability.
We convolve our pixels with a Gaussian smoothing formula and adjust the
smoothing length h to give optimal results.
Let 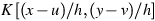 be the smoothing
kernel. This smoothing kernel is then integrated over the camera pixel to
yield an estimate of the flux at points (x,y) for a particular pixel:
be the smoothing
kernel. This smoothing kernel is then integrated over the camera pixel to
yield an estimate of the flux at points (x,y) for a particular pixel:
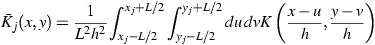 |
 |
(Eq. III.3.b.1) |
where (xj,yj) is the center of the
jth pixel with linear scale L=2´´.
For convenience, we choose a Gaussian for the smoothing kernal K,
which immediately yields:
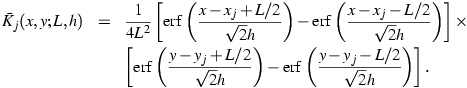 |
 |
(Eq. III.3.b.2) |
The coadded flux estimate for npix pixels with value
m is:
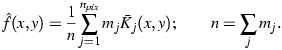 |
 |
(Eq. III.3.b.3) |
Given a coadd pixel of side length l and center at (x,y), the
contribution from the frame pixel j follows by integrating Eq.
III.3.b.2:
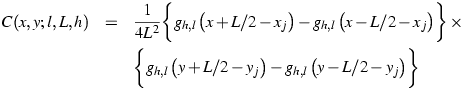 |
 |
(Eq. III.3.b.4) |
where
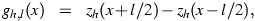 |
 |
(Eq. III.3.b.5) |
and
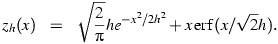 |
 |
(Eq. III.3.b.6) |
The mean integrated squared error,
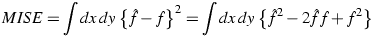 |
 |
(Eq. III.3.b.7) |
where 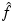 is the estimate and
f is the true flux density, is a standard measure for selecting the
optimal smoothing length. Of course, we do not know the true f, but by
taking the expectation of MISE, we can evaluate the first two terms
from the data.
Based on point sources, the optimal value for h=0.1. An empirical
selection based on the pipeline performance on extended sources suggests
h=0.35. Because the run of MISE for point sources slowly
increases for values larger than the optimal, h=0.35 is still nearly
optimal for point sources, and this value is adopted (see
Figure 2).
is the estimate and
f is the true flux density, is a standard measure for selecting the
optimal smoothing length. Of course, we do not know the true f, but by
taking the expectation of MISE, we can evaluate the first two terms
from the data.
Based on point sources, the optimal value for h=0.1. An empirical
selection based on the pipeline performance on extended sources suggests
h=0.35. Because the run of MISE for point sources slowly
increases for values larger than the optimal, h=0.35 is still nearly
optimal for point sources, and this value is adopted (see
Figure 2).
 |
| Figure 1 |
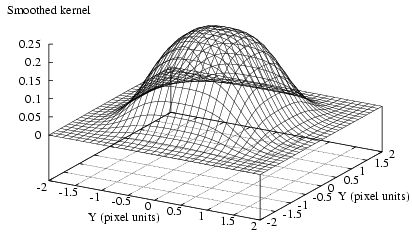 |
Figure 2: Gaussian kernel with h=0.35 convolved over pixel
with active linear size
L=1.0. The mesh diagram shows the
contribution of the flux in the pixel centered
about the origin at arbitrary point (x,y).
|
[Last updated: 1999 May 4, by E. Kopan and M. Weinberg.]
Previous page. Next page.
Return to Explanatory Supplement TOC Page.
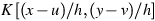 be the smoothing
kernel. This smoothing kernel is then integrated over the camera pixel to
yield an estimate of the flux at points (x,y) for a particular pixel:
be the smoothing
kernel. This smoothing kernel is then integrated over the camera pixel to
yield an estimate of the flux at points (x,y) for a particular pixel:
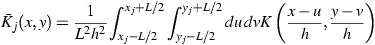

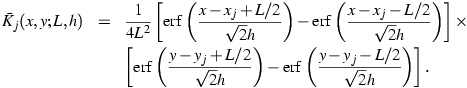

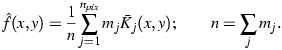

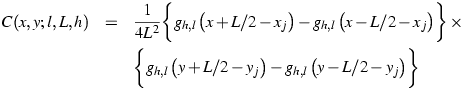

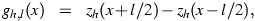

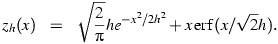

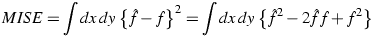

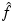 is the estimate and
f is the true flux density, is a standard measure for selecting the
optimal smoothing length. Of course, we do not know the true f, but by
taking the expectation of MISE, we can evaluate the first two terms
from the data.
Based on point sources, the optimal value for h=0.1. An empirical
selection based on the pipeline performance on extended sources suggests
h=0.35. Because the run of MISE for point sources slowly
increases for values larger than the optimal, h=0.35 is still nearly
optimal for point sources, and this value is adopted (see
Figure 2).
is the estimate and
f is the true flux density, is a standard measure for selecting the
optimal smoothing length. Of course, we do not know the true f, but by
taking the expectation of MISE, we can evaluate the first two terms
from the data.
Based on point sources, the optimal value for h=0.1. An empirical
selection based on the pipeline performance on extended sources suggests
h=0.35. Because the run of MISE for point sources slowly
increases for values larger than the optimal, h=0.35 is still nearly
optimal for point sources, and this value is adopted (see
Figure 2).

