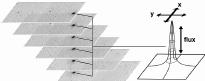
The primary photometry and position estimation algorithm for each candidate detection from the Atlas Images is point source profile-fitting. This provides the most robust estimation for faint sources and objects in denser or more complex environments. Although the detection is done on the coadded Atlas Images, the point source fit is performed directly on the flat-fielded pixel values in a stack of 6 frames, using knowledge of the PSF shape and the relative position offsets for the frames. The latter have already been determined during the Atlas Image generation (cf. IV.3). This is illustrated in Figure 1; the position and amplitude of the source profile is determined during the fitting procedure, but the relative positions of the frames in the stack are held fixed.
 |
| Figure 1 |
We now discuss the mathematical details of the procedure used.
PSF-fitting photometry is based on the data in the neighborhood of each
candidate detection, as defined by a ``data circle'' of 2 pixels,
centered on the nominal location of the detection. We start by
writing a measurement model which expresses
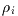 the observed pixel value corresponding to the ith point within the
data circle, in terms of the quantities that we wish to estimate.
For an isolated object, i.e.,
one which is sufficiently distant from its neighbors that there is no
interaction between the corresponding PSFs, these
quantities consist simply of the flux and position of the object.
However, if the point source detection algorithm reports multiple candidates
closer than approximately 5´´ (the precise number varies with the
actual seeing), then the profiles will be fit to each detection simultaneously.
The number of sources being solved for simulaneously is referred to as
the blend number, NB.
the observed pixel value corresponding to the ith point within the
data circle, in terms of the quantities that we wish to estimate.
For an isolated object, i.e.,
one which is sufficiently distant from its neighbors that there is no
interaction between the corresponding PSFs, these
quantities consist simply of the flux and position of the object.
However, if the point source detection algorithm reports multiple candidates
closer than approximately 5´´ (the precise number varies with the
actual seeing), then the profiles will be fit to each detection simultaneously.
The number of sources being solved for simulaneously is referred to as
the blend number, NB.
A suitable measurement model is then:
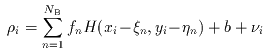 |
 |
(Eq. III.3.c.8) |
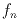 ,
,
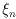 ,
and
,
and 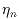 represent the flux and (x,y) location of the nth source in the
blend; (xi,yi) represents the angular position
in the sky corresponding to the ith pixel (obtained from the focal-plane
position and dithering offsets), H(x,y) is the point
spread response (PSF), b is the local background (estimated separately),
and
represent the flux and (x,y) location of the nth source in the
blend; (xi,yi) represents the angular position
in the sky corresponding to the ith pixel (obtained from the focal-plane
position and dithering offsets), H(x,y) is the point
spread response (PSF), b is the local background (estimated separately),
and 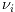 represents
the measurement noise. The latter is modeled as a zero-mean Gaussian random
process whose covariance can be expressed as:
represents
the measurement noise. The latter is modeled as a zero-mean Gaussian random
process whose covariance can be expressed as: |
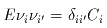 |
(Eq. III.3.c.9) |
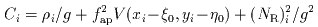 |
 |
(Eq. III.3.c.10) |
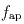 is the estimated flux
density from aperture photometry,
V(x,y) is the PSF variance at offset (x,y) from center
(calculated during the PSF estimation procedure), and
(NR)i is the read noise.
The quantities
is the estimated flux
density from aperture photometry,
V(x,y) is the PSF variance at offset (x,y) from center
(calculated during the PSF estimation procedure), and
(NR)i is the read noise.
The quantities 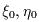 represent the nominal position of the candidate detection.
The error associated with using the nominal rather than true source position
is incorporated in V(x,y).
represent the nominal position of the candidate detection.
The error associated with using the nominal rather than true source position
is incorporated in V(x,y).
The goal of the estimation procedure is to obtain the most probable values
of the quantities 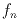 ,
,
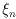 ,
,
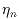 (where n = 1,...,
NB).
To simplify the notation, we will form a vector, z, of unknowns,
whereby the components of z are:
(where n = 1,...,
NB).
To simplify the notation, we will form a vector, z, of unknowns,
whereby the components of z are:
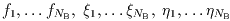 .
Also, we will use
.
Also, we will use 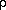 to denote the
vector whose components are
to denote the
vector whose components are
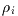 :
i=1,...,M, where M is the number
of pixel values within the data circle. Our goal can then be expressed in
terms of obtaining the most probable value of z
(denoted
:
i=1,...,M, where M is the number
of pixel values within the data circle. Our goal can then be expressed in
terms of obtaining the most probable value of z
(denoted 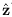 ) conditioned on
) conditioned on
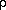 ,
i.e., to maximize the conditional probability
,
i.e., to maximize the conditional probability
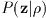 .
If we have no information a priori on the distributions of possible
values of the components of z, then it is appropriate to regard the
a priori probability density distribution of z as flat,
i.e., P(z)= constant. In this case, Bayes' rule tells us that
the most probable value of z can be obtained equally well by maximizing
.
If we have no information a priori on the distributions of possible
values of the components of z, then it is appropriate to regard the
a priori probability density distribution of z as flat,
i.e., P(z)= constant. In this case, Bayes' rule tells us that
the most probable value of z can be obtained equally well by maximizing
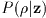 , since it differs from
, since it differs from
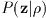 only by an
ignorable constant. This is known as the maximum likelihood procedure, and
is the procedure used in the 2MASS profile fitting photometry. Since the
measurement noise is assumed to be Gaussian, we can write an expression for
only by an
ignorable constant. This is known as the maximum likelihood procedure, and
is the procedure used in the 2MASS profile fitting photometry. Since the
measurement noise is assumed to be Gaussian, we can write an expression for
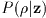 as follows:
as follows:
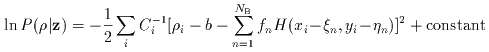 |
 |
(Eq. III.3.c.11) |
The maximization of this expression with respect to z is
actually performed as a minimization of
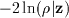 , using the conjugate
gradient method.
, using the conjugate
gradient method.
The next step is to examine the goodness of fit to the data, which is
accomplished by calculating the reduced 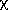 2,
given by:
2,
given by:
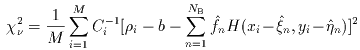 |
 |
(Eq. III.3.c.12) |
If the solution represents a reasonable fit to the data, then
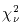 ~1. Otherwise, we would
conclude that
the model involving NB sources is inadequate, which could be
due either to an extended source or a close blend of point sources.
For the initial 2MASS data processing, no attempt is made to deconvolve
single candidates with poor profile fits (i.e., large
~1. Otherwise, we would
conclude that
the model involving NB sources is inadequate, which could be
due either to an extended source or a close blend of point sources.
For the initial 2MASS data processing, no attempt is made to deconvolve
single candidates with poor profile fits (i.e., large
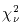 values).
values).
The uncertainties of the estimated quantities can be obtained from the
curvature of ln 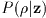 , as
discussed by Whalen (1971, ``Detection of Signals in Noise," Academic Press,
New York). Specifically, we define a matrix
, as
discussed by Whalen (1971, ``Detection of Signals in Noise," Academic Press,
New York). Specifically, we define a matrix 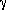 as
follows:
as
follows:
 |
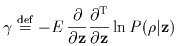 |
(Eq. III.3.c.13) |
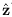 .
.
From Eqs. III.3.c.11 and III.3.c.13, the individual components of
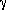 are given by:
are given by:
 |
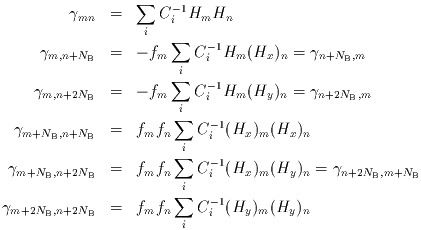 |
(Eq. III.3.c.14-19) |
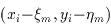 , and
(Hx)m,
(Hy)m denote the corresponding quantities
obtained from partial derivatives of H(x,y) with respect to its two
arguments, respectively.
, and
(Hx)m,
(Hy)m denote the corresponding quantities
obtained from partial derivatives of H(x,y) with respect to its two
arguments, respectively.
The diagonal elements of the inverse of 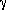 then
correspond to lower limits for the variances of the estimated quantities,
i.e.,
then
correspond to lower limits for the variances of the estimated quantities,
i.e.,
 |
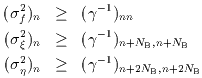 |
(Eq. III.3.c.20 - 22) |
It can be shown that if the measurement model is linear, equality holds in the above expressions. Since the measurement model is linear in flux, equation 20 therefore yields realistic values for the flux uncertainties. In the case of the positional uncertainties, however, the above expressions provide lower limits only.
The blend number, NB is specified in each record of the
Point Source Catalog as "bl_flg" (blend flag), and
indicates the number of candidates fit simultaneously. Blend
flag values >1 are therefore useful as indicators of possible confusion in
regions of high source density. For example,
Figure 2 shows the Ks image of sources 2MASSI J0009220+343350
and 2MASSI J0009260+335945. The former is the brighter of the two
objects, and is a 3-band detection having a bl_flg of "112." The
latter source is the fainter of the pair, is detected only in the H and
Ks bands, and has a bl_flg of "012." Both sources
are clearly visible in all three bands, but the pair was resolved only
in H and Ks. The separation of the pair in Ks
was small enough so that the profile fitting was run simultaneously
on both sources (NB=2), but in H the separation was large
enough that the sources were fitting individually. The
 2
value of the J-fit in the bright source is 6.35, indicating that
the single psf-fit was poor.
2
value of the J-fit in the bright source is 6.35, indicating that
the single psf-fit was poor.
Objects with valid profile-fit R2-R1 photometry (i.e., non-saturated and converged profile fit) have ``rd_flg'' values of ``2'' in the Point Source Catalog record. This corresponds to the great majority of all point sources in the Catalog.
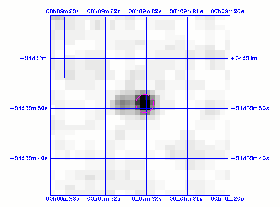 |
| Figure 2 |
i. Point Spread Functions and Seeing Estimation
The source contribution to the profile fit model is proportional to a point-spread-function (PSF) which is taken from a library of PSFs indexed by seeing for each band. PSF's are not derived "on-the-fly" during 2MASS pipeline processing because of the difficulty in automated PSF construction in much of the sky due to both very low and very high source density. PSF-derivation is also a cpu-intensive task, so the use of a PSF library results in much faster processing run times.
The library PSFs corresponding to specific seeing values were constructed empirically using data from single 2MASS calibration scans (cf III.2.c) having that average seeing value. Images of the 50 brightest stars in each scan are centroided and aligning, summed, and finally interpolated into a 0.1´´ grid. In addition to the PSFs themselves, an estimate of the uncertainty in the PSF (the "variance map") is also produced on the same grid and used by the profile fit analysis to estimate the total uncertainties in the resulting estimates. Selection of the calibration scans for PSF generation, and of the PSFs themselves, was based on criteria such as small variability of the seeing parameter during the scan, x- and y- central moments of the stars being equal (typically within 10%), and consistency with other PSFs taken under similar conditions. A single PSF is assumed to accurately characterize the point source profile across the 2MASS focal plane for the purposes of the data processing.
The appropriate PSF is chosen for the profile fitting photometry during the processing of a 2MASS survey scan by estimating the mean point source diameter (seeing) on spatial scales no finer than the length of an Atlas Image, 17´, corresponding to a time interval in the scan of approximately 18 sec. The actual interval used to determine the seeing is driven by source density, and in low star density regions the interval can be up to 3 times longer. If the seeing is variable on timescales shorter than the seeing estimation response time, there can be a photometric error of up to several percent induced by a mismatch between the true image profile and the PSF used in profile-fitting photometry.
[Last Updated: 2000 June 20; by R. Cutri & K. Marsh]