g. Stellar Number Density and Confusion Noise
As the surface density of stars exponentially increases near the disk of the Galaxy, the probability of source contamination increases accordingly. Likewise, near the Galactic plane, faint undetected stars significantly increase the mean "noise" amplitude in the "background" sky. Both surface density affects limit the source detection or completeness, and overall reliability. Confusion arises from the appearance of an interloping star within close proximity to the "beam" or point spread function pattern that induces a significant flux bias (or "deflection") from the non-contaminated flux due to the intended source (in our case, galaxy) near the beam center. A convenient gauge for the severity of contamination or level of source confusion, is the confusion "noise". In more practical form, the confusion noise represents the change in surface brightness (i.e., sensitivity limit) relative to the Galactic pole (where the confusion noise is negligible), expressed in magnitude units. The confusion noise is directly related to the stellar number density. In the 2MASS database the stellar number density is referred to as the "density", representing the base-10 log of the cumulative number of stars per deg2 brighter than Ks=14 mag (see also Table 1). The starcount metric is discussed in detail in IV.5c.
As the confusion noise becomes appreciable, it is one of the primary limits on galaxy detection and reliability. Moreover, confusion decreases the accuracy of both flux and position estimation. It is therefore important to understand the confusion noise in terms of the ability to detect isolated sources and in terms of identification of real extended sources, both of which require threshold adjustment with confusion noise level.
i. Estimation of Confusion Noise
To estimate the additional component of "confusion" noise, we adopt the
methodology of Hacking (1987, PhDT) and Hacking & Houck (1987, ApJS, 63,
311). The idea is to
integrate the expected number of sources (with some flux distribution) within
the 2MASS effective beam,
where N is the integrated stellar number density (in deg2)
at flux f (in mJy). The aggregate variance due to background sources in
the beam, derived from
where Dc represents the outlier or "deflection" cutoff point
(in n-
Appropriate values for 2MASS Ks-band data are the following:
The confusion noise adds in quadrature to the already present background noise,
ii. Confusion Noise, Stellar Density and Galactic Coordinates
For relatively moderate flux ranges (e.g., V < 18; Ks < 14),
basic three-component models of the Galactic stellar distribution adequately
describe the number density of dwarf and giant stars comprising "disk" and
"spheroid" populations (Elias 1978, ApJ, 224, 453; Bahcall & Soneira 1980,
ApJS, 44, 73; Garwood & Jones 1987, PASP, 99, 453). Here we employ a
near-infrared modified variation on the Bahcall
& Soneira model, which predicts the stellar number density with ~90%
accuracy for most of the sky (|b| > 30°) and Ks < 14 mag,
and performs adequately (~80%) for the Galactic plane where patchy extinction
ultimately limits the utility of these simple models. The star-count model
predicts the stellar number density as a function of the Galactic coordinates,
which can then be used to calculate the approximate confusion noise.
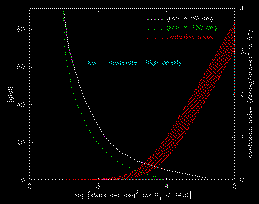
A plot of the stellar number density (see
IV.5c) as a function of the Galactic latitude
along two separate longitudes (50° and 130°) is shown in
Figure 30. The vertical dotted lines
represent the thresholds for what is deemed low stellar number density
(<103.1 stars deg-2), moderate density
(<103.6 stars deg-2), and high density
(>103.6 stars deg-2). The limit on high density is
partly driven by the relative density of triple stars vs. double or single
stars. As triple+ stars become appreciable, the ability to distinguish real
galaxies from close groupings of stars is greatly diminished. Finally, the
confusion noise (
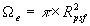, where
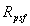represents the effective
radius of the point spread function (typically ~2´´).
We may approximate the stellar flux distribution
with a power law of index 
,
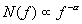
(Eq. IV.5.13)
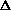f,
d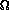
and
the differential stellar number density, is then
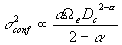
(Eq. IV.5.14)
units; i.e., the detection threshold).
The source density index is approximately
equal to unity (more precisely ~0.85 for high latitude fields) as derived from
the log-log slope of the N vs. Ks cumulative star count
curve, ~0.35 for the NGP and slightly steeper at higher densities (Jarrett
1992, PhDT). Letting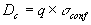 
,
we may express the confusion noise
as a function of the stellar number density, N(flim), at the
limiting flux, flim, and the deflection cutoff, q,
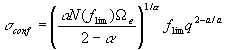
(Eq. IV.5.15)
= 0.9,
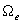= 13.6 arcsec2 (4´´ beam),
flim = 1.8 mJy (corresponding to Ks=14 mag), and
q between 3 and 5; the confusion noise has units of mJy.
,
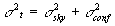raising the overall noise and
surface brightness of the background light. We desire to express the change in
the background surface brightness due to confusion noise as a function
of the stellar number density. We can turn the confusion noise into a surface
brightness by dividing by .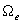
For the
background sky noise we adopt a value of 20.0 mag/pixel (typical for 2MASS 2.2
µm images). To convert the sky noise per pixel to
an equivalent surface brightness within the PSF beam, we need to divide by
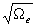to account for the noise limit after
averaging over a 4´´ diameter. Accordingly, we
arrive at a sky noise surface brightness of 21.6 mag/arcsec2,
representing the value at the north Galactic pole (NGP), which is negligibly
affected by confusion from stars. The confusion noise (in
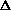mag units) is relative to the NGP sky surface
brightness noise (in a 4´´ diameter beam). The
Ks-band confusion noise as a function of the total integrated
stellar number density (flim < 1.8 mJy, or Ks
< 14 mag) is plotted in
Figure 30, described below, assuming a
beam size of 4´´, = 0.9 and
q between 3 and 5.
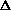mag) appropriate to the
stellar number density is plotted in
Figure 30 (denoted with a cross-hatching, showing the detection threshold
range in q between 3 and 5), with the confusion noise
axis located at the right of the plot. Here the confusion noise (in mag units)
is relative to the equivalent sky background surface brightness
(1- detection limit) measured at high galactic
latitudes (i.e., NGP), equal to 0.0016 mJy (in a 4´´ circular
diameter beam) or 21.6 mag at 2.2 µm. This relative confusion noise is
called the "differential" confusion noise above.
