f. Galaxy Photometry Error Tree
The fundamental limits to 2MASS galaxy photometry are set by the accuracy to which the background level can be determined, by the total signal to noise ratio in the aperture used to report the flux of a galaxy, and by the zero-point calibration used to adjust raw magnitudes onto a standard scale. Most of the time, the dominant error is the Poisson noise due to the background summed over the pixels used to make the photometric measurement and the uncertainty in the standard background removal itself (see IV.5a). However, a significant portion of the 2MASS data is affected by high-frequency background variation, which causes the photometric error to be larger for a small fraction of the galaxies. There are two sources for such background variations, one being atmospheric "airglow" and the other camera hardware related. In the near-infrared, the background levels generally fluctuate due to airglow emission, sometimes at very high spatial frequencies, particularly at 1.6 µm. In addition to airglow, 2MASS images include electronic ("pickup") noise that is correlated and can, at times, be comparable to the airglow component. Electronic pickup refers to image features that are not of astronomical origin, but instead are associated with the camera electronics. These features may manifest as periodic horizontal stripes or abrupt jumps in the background level. The impact is mostly felt in the galaxy photometry, where a systematic bias is introduced. This bias can be as large as 20% in some cases, but is more typically 3 to 7% (usually an overestimate of the galaxy flux). Examples of both forms of background enhancement are given in Figure 29.
i. Summary of Standard Photometric Error
For the usual case where the galaxy flux is negligible compared to the
background flux, the measurement error in summing up the flux over n
pixels in the Atlas image is
where
GALWORKS also models and subtracts variations
in the background using a polynomial fitting scheme described
IV.5a. If
the background variations are small on time scales of a few seconds, the
fitting procedure is limited primarily by the effective RMS in the background
sky noise,
It is clear that the first term dominates the total error except when the
number of pixels within the aperture is very large, n >
104 (corresponding to a circular radius > 40 to 50 pixels).
This also assumes
that background variation is well behaved. Most galaxies detected in 2MASS are
small and faint, so the Poisson noise component (Eq. IV.5.9) should dominate
the total photometric error. Consider for example a Ks=13 mag
galaxy. The integrated flux is ~630 DN (or ~4.5 mJy) using a
typical Ks zero point magnitude of 20.0 mag (relating the calibrated
mag to the raw or "data number" flux; see Eq. IV.5.8). The typical size for a
galaxy of this brightness is about 16´´ in
diameter, corresponding to a circular aperture with ~200 pixels. The typical
Ks background pixel noise is ~1 DN (or 20 mag per
arcsec2). Using Eq. IV.5.10 and the integrated flux of the source,
we compute a SNR of 12.6 to 12.8, where the Poisson component is 25 to 70 times
larger than the background-fit uncertainty (i.e., the noise contribution from
the background fitting procedure is very small, only 1 to 4% of the
total photometric noise). For larger (and hence less common) galaxies,
the size of the galaxy must be greater then ~35´´
in diameter for the uncertainty in the background fit to become appreciable
(>10% of the total).
If the background variation requires a higher-power polynomial than a cubic,
then the error in the background will no longer be determined by the pixel
noise. Instead, the background error will result from the residual error after
a cubic polynomial is fit. This will be the case for severe airglow variation,
which can modulate on high spatial frequency scales (see left panel,
Figure 29), and from correlated
"electronic" noise (see right panel, Figure
29). Both
conditions can easily boost the total photometric noise by >50%.
Unfortunately, the 2MASS data reduction pipeline is not adequately designed to
quantify these severe background variations; and indeed, high-frequency
background variations may go undetected from scan to scan. We are exploring
methods at which detection and correction of severe 'airglow features" may be
possible, particularly for the H-band data. Fortunately, the hardware-induce
background variations are diminishing with maturity of the 2MASS survey.
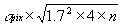
(Eq. IV.5.9)
pix is the measured pixel
noise as measured using an entire Atlas image (512×1024 pixels).
The factor of 1.7 accounts for the smoothing introduced in the
Atlas image by the frame resampling and construction process, and the factor
of 4 results from the correlation of the flux in 1´´ pixels, due to
the 2´´ camera (raw frame).
pix. The fitting
procedure usually can match the background over regions as small as
~2´ to 3´. Empirical tests
indicate that the background fitting procedure is accurate to within 3 to 5%
of the RMS pixel noise (in the absence of abrupt background structure coming
from high-frequency airglow or electronic banding, which is usually the case
for the 2.2µm images). Since errors in the
background contribute systematically to all pixels in a galaxy smaller than
3´, this error contributes in proportion to the
number of pixels n. The total photometric noise variance is the quadratic sum
of these two terms
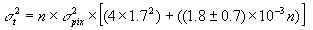
(Eq. IV.5.10)
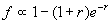
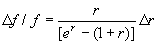
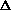r. The typical width or
uncertainty of the circular isophote is about 1´´, so