A postscript copy of the paper with complete details on these results is Carpenter (2001, AJ, 121, 2851).
Even though the IDR2 Catalogs are considered preliminary, as all data will be reprocessed at the completion of the 2MASS observations with a final version of the data reduction pipeline, the data already meets a high degree of global photometric uniformity. It is therefore appropriate to determine the color transformations between the IDR2 and other photometric systems in common use today. These transformation equations were derived using 2MASS observations of the standard stars defining current photometric systems. This exercise necessarily emphasizes recent grids of faint near-infrared standards which have effectively replaced more traditional standards that are usually too bright to be observed with modern instrumentation.
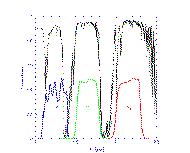
Both the Northern and Southern 2MASS telescopes are outfitted with a similar set of optics, filters, and detectors to observe the J, H, and Ks (``K-short'') bands simultaneously (see Section III.1b). Since the total transmission through the atmosphere and the optical elements essentially define any photometric system, it is instructive to review these characteristics as they pertain to 2MASS and note any substantial differences from other photometric systems. Figure 1 shows the transmission as a function of wavelength through the 2MASS optical path, including the telescope mirror reflectivity, the dewar window, anti-reflection coatings, dichroics, filters, and the NICMOS detector quantum efficiency, but excluding the atmosphere. The dominant source of transmission loss through the optical path is the detector quantum efficiency, which is about 0.6-0.65 in the J, H, and Ks bandpasses. A model atmospheric transmission for the mean conditions at Mt. Hopkins is shown separately in Figure 1 as indicated by the thin solid line. The atmospheric transmission data, kindly provided by Martin Cohen, was computed using the USAF PLEXUS code and binned to a resolution of 0.002 micron for display purposes. The transmission curves for both the optical elements and the atmosphere are tabulated in Section III.1b. The primary distinction between 2MASS and many other photometric systems is that the 2MASS Ks filter transmission was specially designed to cut off at 2.3 micron in order to reduce the noise contribution from the thermal background. In this manner, the noise in the Ks band observations will be less sensitive to variations in the ambient temperature, allowing for a more uniform photometric survey. A similar filter has been adopted by the DENIS survey and also was incorporated into the standard star observations by Persson et al. (1998, AJ, 116, 2475). By comparison, more traditional Johnson K filters have significant transmission out to 2.4 microns. We therefore distinguish the 2MASS Ks filter from the Johnson K filter when presenting the color transformations.
As shown in Figure 1, the short and long wavelength cutoff of the 2MASS J filter extends into the atmospheric water absorption features at 1.1 micron and 1.4 micron. In dry weather, the transmission at these wavelengths can be significant compared to typical conditions, implying that the effective J band wavelength, calibration zero-points, and possibly color transformations will depend on the atmospheric water vapor content. Indeed, the J band calibration zero-points often show smooth variations within a night as large as 0.1 magnitudes, and seasonal variations in the average zero-point as large as 0.2 magnitudes are observed. While the 2MASS survey does not record the atmospheric water vapor content directly, these zero-point variations are presumably due to changes in the amount of water vapor.
The above discussion indicates that various aspects of 2MASS photometry need to be investigated before deriving the color transformations between 2MASS and other photometric systems, namely,

|
| Figure 1 |
To examine any possible temporal variations in the observed stellar colors, 2MASS photometry in a 1° × 6 ° region near the Galactic plane was analyzed that has been observed on two occasions with the Mt. Hopkins telescope, once on June 12, 1997 near the start of Northern survey operations, and again on May 24, 2000. Thus comparison of these sets of observations will indicate any change in the photometry over nearly a 3-year time period. Besides the long time baseline, this field was chosen since the J-band calibration zero-point on the two nights is the same to within 0.01 mag, suggesting that the atmospheric conditions were similar for both sets of observations (see above). A similar sized region with large differences in the J-band zero-points is analyzed in the following section.
Sources were selected from both survey nights that satisfied the following
criteria:
(1) the source is free of any flags from the 2MASS data processing pipeline
that indicate the photometry may be contaminated by a nearby star;
(2) if the magnitudes were computed using PSF fitting photometry, the reduced
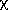 2 from the PSF fit is
2 from the PSF fit is
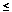 15 in each of the
J, H, and Ks
bands were matched with a source in the second observational set using a
1" search radius. A total of 34,083 sources were matched in this
manner. The absolute value of the average photometric offset between the two
nights, computed by averaging the difference in photometry for all matched
sources, is 0.025, 0.001, and 0.002 mag at J, H, and Ks band
respectively. Measured relative to the zero-point calibration uncertainties,
the offsets are 0.8
15 in each of the
J, H, and Ks
bands were matched with a source in the second observational set using a
1" search radius. A total of 34,083 sources were matched in this
manner. The absolute value of the average photometric offset between the two
nights, computed by averaging the difference in photometry for all matched
sources, is 0.025, 0.001, and 0.002 mag at J, H, and Ks band
respectively. Measured relative to the zero-point calibration uncertainties,
the offsets are 0.8  , 0.04
, 0.04  ,
and 0.09
,
and 0.09  . Therefore, any
difference in the photometric zero-points between the two nights is within the
nightly zero-point uncertainties. The zero-point offsets were removed by
adding a constant to the first night of observations such that the following
analysis compares only the difference the stellar colors. No offsets have been
applied to the 2MASS data, however, when comparing the 2MASS photometry with
other photometric systems.
. Therefore, any
difference in the photometric zero-points between the two nights is within the
nightly zero-point uncertainties. The zero-point offsets were removed by
adding a constant to the first night of observations such that the following
analysis compares only the difference the stellar colors. No offsets have been
applied to the 2MASS data, however, when comparing the 2MASS photometry with
other photometric systems.
Linear fits to the J-K, J-H, and H-K colors between the two sets of
observations were performed using the FITEXY program (Press et al. 1992,
Numerical Recipes in C) that incorporates uncertainties from both
measurements. The reduced 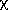 2 is about
0.7 for each of the fits,
indicating that the colors are well modeled by a linear relation and that the
residuals are consistent with random noise. Based on the fit, the difference
in the observed colors between observations taken about 3 years apart is less
than 0.01 mag for J-H < 1.3 and J-Ks < 1.8. The results for the
H-Ks fit are not meaningful since the observed dispersion in the
colors (0.089 mag) is only slightly larger than the expected dispersion
(0.066 mag) due to photometric noise, such that there is little intrinsic
variations in the H-Ks colors for this field. Nevertheless,
the strong similarity between the J-H and J-Ks colors suggest that
any intrinsic variations in the H-Ks colors must also be small.
Thus any temporal changes in the 2MASS color system as judged from the
J-H and J-Ks results are comparable to the minimum photometric
uncertainties (about 0.02 mag) for any individual star.
2 is about
0.7 for each of the fits,
indicating that the colors are well modeled by a linear relation and that the
residuals are consistent with random noise. Based on the fit, the difference
in the observed colors between observations taken about 3 years apart is less
than 0.01 mag for J-H < 1.3 and J-Ks < 1.8. The results for the
H-Ks fit are not meaningful since the observed dispersion in the
colors (0.089 mag) is only slightly larger than the expected dispersion
(0.066 mag) due to photometric noise, such that there is little intrinsic
variations in the H-Ks colors for this field. Nevertheless,
the strong similarity between the J-H and J-Ks colors suggest that
any intrinsic variations in the H-Ks colors must also be small.
Thus any temporal changes in the 2MASS color system as judged from the
J-H and J-Ks results are comparable to the minimum photometric
uncertainties (about 0.02 mag) for any individual star.
As discussed above, the effective transmission
through the 2MASS J band filter depends on the amount of atmospheric water
vapor. Variations in the water vapor content may lead to changes in the J band
zero-point calibration and possible introduce additional color terms for the
survey data. To quantify this effect, we compared 2MASS photometry for another
1x6 sq. deg. region that was observed on 2 occasions by the
Northern survey telescope in which the J band zero-point between the 2
nights differed by 0.16 mag, presumably due to differences in atmospheric water
vapor content. A total of 49,389 stars were identified between the two
observations using the criteria described
above. The
average photometric offsets between the two observations measured relative to
the zero-point calibration uncertainties are 0.5  ,
1.1
,
1.1  , and 1.6
, and 1.6  for J, H, and Ks, respectively. Thus the photometric
offsets
were consistent within the calibration uncertainties, and the zero-points
differences were removed before comparing the near-infrared colors (see
above).
The reduced
for J, H, and Ks, respectively. Thus the photometric
offsets
were consistent within the calibration uncertainties, and the zero-points
differences were removed before comparing the near-infrared colors (see
above).
The reduced 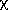 2 is about 0.9 for each of
the linear fits to the
near-infrared colors, again indicating that the correlation between the two
sets of observations is well represented by a linear relation.
Based on the linear fit, the difference in the
observed colors between the two observations is less than 0.014 mag for
J-H < 3.2 mag, less than 0.021 for J-Ks < 4.7, and
less than 0.01 mag for H-Ks < 1.5. Thus no significant change
relative to the photometric uncertainties for an individual star was found in
the 2MASS photometric system in varying atmospheric conditions.
2 is about 0.9 for each of
the linear fits to the
near-infrared colors, again indicating that the correlation between the two
sets of observations is well represented by a linear relation.
Based on the linear fit, the difference in the
observed colors between the two observations is less than 0.014 mag for
J-H < 3.2 mag, less than 0.021 for J-Ks < 4.7, and
less than 0.01 mag for H-Ks < 1.5. Thus no significant change
relative to the photometric uncertainties for an individual star was found in
the 2MASS photometric system in varying atmospheric conditions.
iv. Comparison between the 2MASS South and North Surveys
While much effort has been placed on making the Northern and Southern
operations as identical as possible, small differences in the color systems
between the two surveys may still potentially exist.
Any differences in the observed stellar colors between the northern and
southern hemisphere surveys have been evaluated using 5 fields with
declinations between -9 deg and +3 deg that were observed by both
telescopes between November 1998 and July 2000. A total of 155,011 point
sources were matched between the northern and southern survey data using the
criteria described above.
The average photometric offset,
where the offset is in the sense of the magnitude observed in the north minus
the magnitude observed from the south, ranges from -0.011 to 0.039 mag
among the three bands. Measured relative to the nightly 1- zero-point calibration uncertainties, the offsets range from -0.45
zero-point calibration uncertainties, the offsets range from -0.45  to 1.9
to 1.9  . These photometric zero-point offsets for
the 5 fields are within
the uncertainties of the nightly calibration, and the offsets have been
applied to the northern data on a night-by-night basis.
Figure 2
compares the observed J-Ka, J-H, and H-Ks colors from
the northern and southern survey telescopes. In each figure, the contours
represent the density of points in the particular diagram, and the dashed line
indicates the expected relation if the near-infrared colors are equal. The
derived linear relation between the two observations are
. These photometric zero-point offsets for
the 5 fields are within
the uncertainties of the nightly calibration, and the offsets have been
applied to the northern data on a night-by-night basis.
Figure 2
compares the observed J-Ka, J-H, and H-Ks colors from
the northern and southern survey telescopes. In each figure, the contours
represent the density of points in the particular diagram, and the dashed line
indicates the expected relation if the near-infrared colors are equal. The
derived linear relation between the two observations are
| (J-Ks)North | = | (1.000 ± 0.001) (J-Ks)South | + | (-0.001 ± 0.001) |
| (J-H)North | = | (1.002 ± 0.001) (J-H)South | + | (-0.003 ± 0.001) |
| (H-Ks)North | = | (1.009 ± 0.001) (H-Ks)South | + | (-0.001 ± 0.001) |
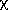 2 from each of the fits
is about 0.9.
These equations indicate that the J-Ks and J-H colors from the
Northern and Southern surveys are statistically indistinguishable. The slope
in the H-Ks transformation, if significant, implies that the
maximum H-Ks color difference between the northern and southern
survey data over the range of colors shown in
Figure 2 is
0.012 mag, which is within the nightly calibration uncertainties for any
individual star. Therefore, it is assumed that the 2MASS North and South
colors systems are identical in the following analysis.
2 from each of the fits
is about 0.9.
These equations indicate that the J-Ks and J-H colors from the
Northern and Southern surveys are statistically indistinguishable. The slope
in the H-Ks transformation, if significant, implies that the
maximum H-Ks color difference between the northern and southern
survey data over the range of colors shown in
Figure 2 is
0.012 mag, which is within the nightly calibration uncertainties for any
individual star. Therefore, it is assumed that the 2MASS North and South
colors systems are identical in the following analysis.

|
| Figure 2 |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Notes to Table 16: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a. Goodness-of-fit-results are for the SAAO vs. Koornneef fit. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The color transformations between 2MASS and the photometric systems summarized
in Table 1 were derived by making a linear fit between the published standard
star photometry (or in the case of DENIS, publicly available catalog data) and
the 2MASS observations of
these stars. The specific variables included in the linear fit are
(Ks)2MASS - Kstd vs. (J-K)std,
(J-Ks)2MASS vs. (J-K)std,
(J-H)2MASS vs. (J-H)std,
and
(H-Ks)2MASS vs. (H-K)std,
where std, treated as the X-variable, represents the standard star
photometry for the appropriate photometric system. The transformation equations were
derived using the routine FITEXY (Press et al. 1992) that minimizes the
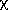 2 between the observations and a
straight-line model. The
uncertainties in both the 2MASS and published photometry are used to evaluate
the
2 between the observations and a
straight-line model. The
uncertainties in both the 2MASS and published photometry are used to evaluate
the 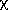 2 merit function. After examining the
residuals from the fit,
sources with large discrepancies between the 2MASS and published
photometry were removed and the fit was re-derived. Any sources removed from
the analysis are noted in
Carpenter (2001).
Table 16 summarizes the goodness-of-fit parameters from the linear fit,
including the reduced
2 merit function. After examining the
residuals from the fit,
sources with large discrepancies between the 2MASS and published
photometry were removed and the fit was re-derived. Any sources removed from
the analysis are noted in
Carpenter (2001).
Table 16 summarizes the goodness-of-fit parameters from the linear fit,
including the reduced 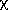 2 of the residuals
and the probability
(q, 0
2 of the residuals
and the probability
(q, 0 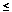 q
q 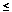 1)
that the reduced
1)
that the reduced 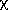 2 can be
exceeded by chance for gaussian distributed noise. The larger the value of
q, the more likely the residuals are consistent with random noise.
Table 16 indicates that with the exception of the DENIS-2MASS fit (see
discussion below), the 2MASS and published photometry are reasonably described
by a linear relationship and the residuals can be explained by photometric
noise. The large reduced
2 can be
exceeded by chance for gaussian distributed noise. The larger the value of
q, the more likely the residuals are consistent with random noise.
Table 16 indicates that with the exception of the DENIS-2MASS fit (see
discussion below), the 2MASS and published photometry are reasonably described
by a linear relationship and the residuals can be explained by photometric
noise. The large reduced  2 values
indicate that the uncertainties in
the fitted parameters for the 2MASS-DENIS transformations are underestimated,
perhaps by as much as about sqrt(2).
The residuals for the K-band transformations tend to have larger reduced
2 values
indicate that the uncertainties in
the fitted parameters for the 2MASS-DENIS transformations are underestimated,
perhaps by as much as about sqrt(2).
The residuals for the K-band transformations tend to have larger reduced
 2 values than that for the color
transformations, especially for
photometric systems that incorporate very red infrared standards. As discussed
by Elias et al. (1983; see also Persson et al. 1998) these red standards tend
to be near star forming regions and have a greater probability of being
variable stars. If any of the red standards do have low amplitude variability,
the magnitude transformations will be most affected since the J-, H-, and
K-band magnitudes will vary simultaneously and produce smaller color changes.
2 values than that for the color
transformations, especially for
photometric systems that incorporate very red infrared standards. As discussed
by Elias et al. (1983; see also Persson et al. 1998) these red standards tend
to be near star forming regions and have a greater probability of being
variable stars. If any of the red standards do have low amplitude variability,
the magnitude transformations will be most affected since the J-, H-, and
K-band magnitudes will vary simultaneously and produce smaller color changes.
To emphasize that the derived color transformations are valid only for the colors spanned by the published photometry, Figure 3 shows the range of J-K colors contained in the data analyzed here for each photometric system. The appropriate ranges for the J-H and H-K colors can be obtained from inspection of Figures 4-14. In addition, these transformations equations may not apply for objects that exhibit complex spectral energy distributions (e.g., T dwarfs). For these objects, the transformation equations will be sensitive to the exact spectral features that are within the filter transmission curve.

|
| Figure 3 |
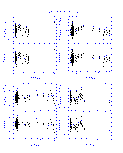
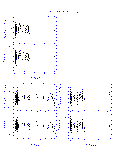
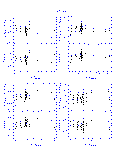
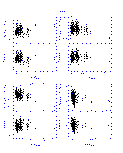
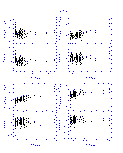
The results from the linear fits are summarized graphically in Figures 4-14 below. In displaying the results, the data are shown as the difference between the 2MASS and standard star photometry as a function of the standard star photometry in order to emphasize subtle, systematic photometric differences. This implies that the X and Y axes are correlated in the plots, which can create artificial trends with slope of -1.0 if the noise in the data exceeds the dynamic range in colors. This effect was quite apparent in the DENIS-2MASS comparisons since the DENIS data have lower signal to noise typically than the 2MASS photometry. For the DENIS results only, the 2MASS photometry is plotted along the X-axis.
The vertical and horizontal bars in Figures 4-14 indicate the 1- photometric uncertainties, although the uncertainties along the X-axis
are often smaller then the symbol size given the dynamic range in the plots.
The upper left panel in each figures plots the difference in the K-band
magnitudes as a function of the J-K color, and the remaining panels directly
compare the J-H, J-K, and H-K colors. The dotted line in the upper portion of
each panel shows the derived transformation between the appropriate photometric
system and 2MASS. The bottom portion of each panel shows the residuals from
the fit, where the horizontal dotted line at zero is drawn for reference.
photometric uncertainties, although the uncertainties along the X-axis
are often smaller then the symbol size given the dynamic range in the plots.
The upper left panel in each figures plots the difference in the K-band
magnitudes as a function of the J-K color, and the remaining panels directly
compare the J-H, J-K, and H-K colors. The dotted line in the upper portion of
each panel shows the derived transformation between the appropriate photometric
system and 2MASS. The bottom portion of each panel shows the residuals from
the fit, where the horizontal dotted line at zero is drawn for reference.
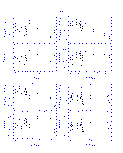
|
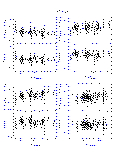
|
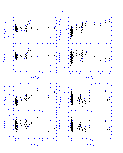
|
| Figure 4 | Figure 5 | Figure 6 |
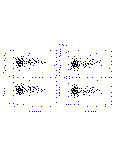
|
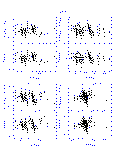
|
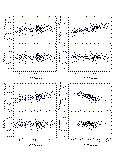
|
| Figure 7 | Figure 8 | Figure 9 |
|
|
|
| Figure 10 | Figure 11 | Figure 12 |
|
|
| Figure 13 | Figure 14 |
| 2MASS - AAO | |||||||
|---|---|---|---|---|---|---|---|
| (Ks)2MASS | = | KAAO | + | (-0.032 ± 0.012) | + | (-0.021 ± 0.008)(J-K)AAO | |
| (J-H)2MASS | = | (0.924 ± 0.015)(J-H)AAO | + | (0.000 ± 0.016) | |||
| (J-Ks)2MASS | = | (0.943 ± 0.009)(J-K)AAO | + | (0.024 ± 0.014) | |||
| (H-Ks)2MASS | = | (0.974 ± 0.033)(H-K)AAO | + | (0.032 ± 0.016) | |||
| 2MASS - ARNICA | |||||||
| (Ks)2MASS | = | KARNICA | + | (0.012 ± 0.006) | + | (-0.024 ± 0.011)(J-K)ARNICA | |
| (J-H)2MASS | = | (1.054 ± 0.020)(J-H)ARNICA | + | (-0.025 ± 0.008) | |||
| (J-Ks)2MASS | = | (1.056 ± 0.016)(J-K)ARNICA | + | (-0.018 ± 0.008) | |||
| (H-Ks)2MASS | = | (1.059 ± 0.070)(H-K)ARNICA | + | (0.007 ± 0.008) | |||
| 2MASS - Bessell & Brett | |||||||
| (Ks)2MASS | = | KBB | + | (-0.044 ± 0.003) | + | (0.000 ± 0.005)(J-K)BB | |
| (J-H)2MASS | = | (0.980 ± 0.009)(J-H)BB | + | (-0.045 ± 0.006) | |||
| (J-Ks)2MASS | = | (0.972 ± 0.006)(J-K)BB | + | (-0.011 ± 0.005) | |||
| (H-Ks)2MASS | = | (0.996 ± 0.019)(H-K)BB | + | (0.028 ± 0.005) | |||
| 2MASS - CIT | |||||||
| (Ks)2MASS | = | KCIT | + | (-0.024 ± 0.003) | + | (0.000 ± 0.005)(J-K)CIT | |
| (J-H)2MASS | = | (1.076 ± 0.010)(J-H)CIT | + | (-0.043 ± 0.006) | |||
| (J-Ks)2MASS | = | (1.056 ± 0.006)(J-K)CIT | + | (-0.013 ± 0.005) | |||
| (H-Ks)2MASS | = | (1.026 ± 0.020)(H-K)CIT | + | (0.028 ± 0.005) | |||
| 2MASS - DENIS | |||||||
| (Ks)2MASS | = | (Ks)DENIS | + | (-0.024 ± 0.006) | + | (0.006 ± 0.004)(J-Ks)DENIS | |
| (J-Ks)2MASS | = | (0.981 ± 0.006)(J-Ks)DENIS | + | (0.023 ± 0.009) | |||
| 2MASS - ESO | |||||||
| (Ks)2MASS | = | KESO | + | (-0.045 ± 0.004) | + | (0.005 ± 0.011)(J-K)ESO | |
| (J-H)2MASS | = | (0.983 ± 0.030)(J-H)ESO | + | (-0.049 ± 0.008) | |||
| (J-Ks)2MASS | = | (0.956 ± 0.017)(J-K)ESO | + | (-0.008 ± 0.006) | |||
| (H-Ks)2MASS | = | (0.956 ± 0.126)(H-K)ESO | + | (0.034 ± 0.006) | |||
| 2MASS - Koornneef | |||||||
| (Ks)2MASS | = | KKoornneef | + | (-0.047 ± 0.006) | + | (0.039 ± 0.019)(J-K)Koornneef | |
| (J-H)2MASS | = | (1.024 ± 0.024)(J-H)Koornneef | + | (-0.045 ± 0.006) | |||
| (J-Ks)2MASS | = | (0.970 ± 0.015)(J-K)Koornneef | + | (-0.017 ± 0.005) | |||
| (H-Ks)2MASS | = | (0.792 ± 0.056)(H-K)Koornneef | + | (0.027 ± 0.005) | |||
| 2MASS-LCO | |||||||
| (Ks)2MASS | = | KLCO | + | (-0.006 ± 0.004) | + | (-0.001 ± 0.002)(J-K)LCO | |
| (J-H)2MASS | = | (0.995 ± 0.006)(J-H)LCO | + | (0.002 ± 0.006) | |||
| (J-Ks)2MASS | = | (1.013 ± 0.005)(J-K)LCO | + | (-0.007 ± 0.006) | |||
| (H-Ks)2MASS | = | (1.008 ± 0.010)(H-K)LCO | + | (0.002 ± 0.005) | |||
| (Ks)2MASS | = | (Ks)LCO | + | (-0.010 ± 0.004) | + | (-0.002 ± 0.002)(J-Ks)LCO | |
| (J-Ks)2MASS | = | (1.007 ± 0.005)(J-Ks)LCO | + | (0.002 ± 0.006) | |||
| (H-Ks)2MASS | = | (1.019 ± 0.010)(H-Ks)LCO | + | (0.005 ± 0.005) | |||
| 2MASS - MSSSO | |||||||
| (Ks)2MASS | = | KMSSSO | + | (-0.023 ± 0.008) | + | (-0.021 ± 0.006)(J-K)MSSSO | |
| (J-H)2MASS | = | (0.991 ± 0.014) (J-H)MSSSO | + | (-0.010 ± 0.014) | |||
| (J-Ks)2MASS | = | (1.005 ± 0.008)(J-K)MSSSO | + | (0.011 ± 0.011) | |||
| (H-Ks)2MASS | = | (1.037 ± 0.029)(H-K)MSSSO | + | (0.019 ± 0.012) | |||
| 2MASS - SAAO | |||||||
| (Ks)2MASS | = | KSAAO | + | (-0.025 ± 0.004) | + | (0.020 ± 0.007)(J-K)SAAO | |
| (J-H)2MASS | = | (0.949 ± 0.018)(J-H)SAAO | + | (-0.054 ± 0.006) | |||
| (J-Ks)2MASS | = | (0.940 ± 0.010(J-K)SAAO | + | (-0.011 ± 0.005) | |||
| (H-Ks)2MASS | = | (0.961 ± 0.036)(H-K)SAAO | + | (0.040 ± 0.005) | |||
| 2MASS - UKIRT | |||||||
| (Ks)2MASS | = | KUKIRT | + | (0.002 ± 0.004) | + | (0.004 ± 0.006)(J-K)UKIRT | |
| (J-H)2MASS | = | (1.069 ± 0.015)(J-H)UKIRT | + | (-0.027 ± 0.007) | |||
| (J-Ks)2MASS | = | (1.069 ± 0.011)(J-K)UKIRT | + | (-0.012 ± 0.006) | |||
| (H-Ks)2MASS | = | (1.062 ± 0.027)(H-K)UKIRT | + | (0.017 ± 0.005) | |||
[Last Updated: 2001 Jan 25 by J. Carpenter (jmc@astro.caltech.edu). Modified 2001 Jan 29 by S. Van Dyk.]